Inversibilité de l'exponentielle d'un endomorphisme nilpotent

[Nightmare]

Soit u un endomorphisme nilpotent, on note

Qui est en fait une somme finie puisque u est nilpotent

Il s'agit de montrer que

Suspense... :lol3:

[Nightmare]

Je comprends pas trop, sans topologie, quel sens donnes-tu à la convergence de la série?

[Nightmare]

La nilpotence assure que ce n'est pas une série mais une somme.

Exact, tu n'avais marqué que 3 lignes dans ton premier post et j'ai quand même réussi à faire l'impasse sur une :lol3:

Bref, je réfléchis à une autre preuve que la tienne.

[ffpower]

Si je ne m abuse,-u est nilpotant, donc e^{-u} est bien définie, et u et -u commutent, donc on peut démontrer de maniere classique que e^u o e^{-u}=Id
Donc je vois pas quel est le probleme particulier dans ce cadre, plus que dans les autres..

[Finrod]

Il me semble que l'on peut utiliser que toute valeur propre de ton polynôme en u (disons P pour faire cours) est de la forme P(a) où a est une valeur propre de u.

ça se fait à la main.

Après, il suffit de regarder les racines de P. Je ne sais pas si cette solution va marcher mais j'essai.

[Finrod]

C'est bon ma méthode marce, je viens de me souvenir qu'un endomorphisme nilpotent n'a que 0 comme valeur propore et P(0) = 1 est non nul donc P(u) n'admet pas 0 comme valeur propre.

edit: prems :zen: ?

edit 2: Je ne voit pas comment simplifier facilement le calcul du produit a moins que l'égalité soit toujours ok.

[Finrod]

Oui! Ton idée m'est venue sous la douche (d'où l'importance de l'hygiene !) Je me suis emmêlée les pinceaux entre "réciproque" et "inverse"

Merci d'avoir confirmé !

moi, je vais bouder

[abcd22]

C'est bon ma méthode marce, je viens de me souvenir qu'un endomorphisme nilpotent n'a que 0 comme valeur propore et P(0) = 1 est non nul donc P(u) n'admet pas 0 comme valeur propre.

Oui mais cela ne suffit pas à montrer que P(u) est un isomorphisme car on peut être en dimension infinie, et dans ce cas injectif n'implique pas surjectif.

edit 2: Je ne voit pas comment simplifier facilement le calcul du produit a moins que l'égalité soit toujours ok.

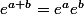
est vraie dès que a et b commutent.

[Finrod]

C'est vrai, mais ici je pense que ça marche même en dimension infinie car la seule valeur propre est 1. On doit donc pouvoir montrer la surjectivité assez facilement. (arête moi si j'ai dit une annerie).

et j'ai l'impression qu'il faut redémontrer la formule dans la mesure ou l'exp n'est définie ici que pour les nilpotens sauf si l'on considère les séries formelles.

edit : en même temps, je n'ai jamais cherché à savoir comment fonctionnent les vp en dim infinie... donc je ne saurais pas le démontrer.

L'ex classique a (virtuellement) une "matrice" triangulaire ou il n'y a que des 0 sur la diagonale. Pourtant il est injectif.

[Ben314]

Salut,
Je rajouterais un point de détail à ce qu'à dit abcd22 :
lorsque a et b commutent exp(a+b)=exp(a)exp(b) à condition que la topologie sur l'espace donne la convergence des séries....

Pour Finrod, il faut faire un peu attention à la notion de valaurs propres en dimension infinie, je ne trouve pas immédiatement d'endomorphisme avec comme seule valeur propre 1 et non surjectif, mais, sur l'e.v. des suites réelles, que pense tu des valeurs propres de l'endomorphisme :
(Un)n -> (Vn)n où Vo=0 et Vn=U(n-1) pour n>0 ?

[Finrod]

Ton ex n'est pas injectif Ben, il a une vp nulle. J'en ai édité un aussi juste au dessus, avec "+1" au lieu de "-1"

[Ben314]

Ton ex n'est pas injectif Ben, il a une vp nulle.

Tu peut me donner une valeur propre de cet endomorphisme ? Laquelle ?

[Finrod]

Non ok c'est bon, tu as donné le même ex que moi en fait, j'ai juste fait une petite crise de dyslexie.

Maintenant que tu le dis, c'est vrai que dans un lointain souvenir, certains endomorphismes n'ont pas de vp en dimension infinie.