Bonjour,
Je suis face a un problème qui me dépasse !
j'ai un repère orthonormé.
Une ellipse dont je connais le demi-grand axe, le demi-petit axe, et l'ordonnée de son centre mais pas l'abscisse.
Une droite quelconque dont je connais toutes les informations, et celle-ci est tangente a l'ellipse en un point que je ne connais pas non plus.
Mon but étant de connaitre l'abscisse du centre de mon ellipse ainsi que les coordonnée du point de tangence.
En espérant qu'une bonne âme aura quelque piste pour m aider a résoudre cette énigme...
Ellipse et tangente
8 messages
- Page 1 sur 1
salut,
une idée, mais j'ai pas testé si ca marchait :
tu prends leq de l'ellipse :
Ici, vu que tu connais l'ordonnée y du centre de l'ellipse, faut se ramener avec la nouvelle origine dans le centre de l'ellipse. mais bon.
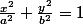
On isole y :
 = \pm b \sqrt{1 - \frac{x^2}{a^2}})
Ensuite, on calcule la tangente T en tout point a de lellipse :
(x-a)+y(a))
On sait que la droite est tangente a lellipse, donc elle a même coeff directeur.
On déduit = a_i) ,
,  étant le coeff dir de ta droite.
étant le coeff dir de ta droite.
On cherche donc x tel que
 = a_i) A tous les coups, on trouve deux solutions possibles. Pis jme suis arreté là. J'espère que ca peut t'aider
A tous les coups, on trouve deux solutions possibles. Pis jme suis arreté là. J'espère que ca peut t'aider 
une idée, mais j'ai pas testé si ca marchait :
tu prends leq de l'ellipse :
Ici, vu que tu connais l'ordonnée y du centre de l'ellipse, faut se ramener avec la nouvelle origine dans le centre de l'ellipse. mais bon.
On isole y :
Ensuite, on calcule la tangente T en tout point a de lellipse :
On sait que la droite est tangente a lellipse, donc elle a même coeff directeur.
On déduit
On cherche donc x tel que
la vie est une fête 
Les axes de l'ellipse sont-il // aux axes du repère ?
Supposons que oui ...
Coordonnée du centre de l'ellipse (Xc ; Yc) avec Yc connu et Xc inconnu.
a et b étant connu, l'équation de l'ellipse est :
(x - Xc)²/a² + (y - Yc)²/b² = 1
Soit y = Ax + B l'équation de la droite tangente à l'ellipse. (A et B connus)
Le système :
(x - Xc)²/a² + (y - Yc)²/b² = 1
y = Ax + B
Doit avoir une solution double -->
(x - Xc)²/a² + (Ax + B - Yc)²/b² = 1
Tu développes et tu as une équation du second degré en x.
Comme la solution de cette équation doit être double, son discriminant est nul
En exprimant cela tu devrais trouver Xc. (0, 1 ou 2 valeurs possibles)
Et ensuite, avec cette ou ces valeurs de Xc, le(s) doublet (s) (x,y) solution(s) du système correspondra(ont) au point de tangeance.
@@@@@@
Si les axes de l'ellipse ne sont pas // aux axes du repère, alors je pense qu'il manque des données pour résoudre le problème.
:zen:
Supposons que oui ...
Coordonnée du centre de l'ellipse (Xc ; Yc) avec Yc connu et Xc inconnu.
a et b étant connu, l'équation de l'ellipse est :
(x - Xc)²/a² + (y - Yc)²/b² = 1
Soit y = Ax + B l'équation de la droite tangente à l'ellipse. (A et B connus)
Le système :
(x - Xc)²/a² + (y - Yc)²/b² = 1
y = Ax + B
Doit avoir une solution double -->
(x - Xc)²/a² + (Ax + B - Yc)²/b² = 1
Tu développes et tu as une équation du second degré en x.
Comme la solution de cette équation doit être double, son discriminant est nul
En exprimant cela tu devrais trouver Xc. (0, 1 ou 2 valeurs possibles)
Et ensuite, avec cette ou ces valeurs de Xc, le(s) doublet (s) (x,y) solution(s) du système correspondra(ont) au point de tangeance.
@@@@@@
Si les axes de l'ellipse ne sont pas // aux axes du repère, alors je pense qu'il manque des données pour résoudre le problème.
:zen:
Avec l'aide et les conseils que vous m'avez donné, j'ai repris les chose du début.
Je considère que j'ai ma droite d: y=mx+m' dans (O,i,j) où O(O,0)
j'ai une ellipse x²/a² + y²/b²=1 dans le repère (O',i,j) où O'(x0,0)
par conséquent j'en déduit l'équation de ma droite dans (O',i,j), j'obtiens:
y=mx+m'+x0
j'injecte ce résultat dans ma formule d'ellipse :
x²/a²+(mx+m'+x0)/b² = 1
étant donné que ma droite d est une tangente, je veux une seule solution a cette équation donc
delta =0
donc je cherche x0 tel que delta=0
donc j'obtiens l'équation suivante :
m²/b4-4*1/a²*( (m'+x0)/b² -1) = 0
et j'arrive donc à x0= (a²m²-4m'b²+4b4)/4b²
Or si je reprend un exemple simple et concret (http://serge.mehl.free.fr/exos/exos_gif/CerMonge1.gif )
ou je considére que ma droite d correspond a la droite PM de l'exemple avec comme équation de droite y=-1/2*x+5/2
j'obtiens x0 = 105/64 = 1.64
Je suis un peu désuvré face a ça ...
Je considère que j'ai ma droite d: y=mx+m' dans (O,i,j) où O(O,0)
j'ai une ellipse x²/a² + y²/b²=1 dans le repère (O',i,j) où O'(x0,0)
par conséquent j'en déduit l'équation de ma droite dans (O',i,j), j'obtiens:
y=mx+m'+x0
j'injecte ce résultat dans ma formule d'ellipse :
x²/a²+(mx+m'+x0)/b² = 1
étant donné que ma droite d est une tangente, je veux une seule solution a cette équation donc
delta =0
donc je cherche x0 tel que delta=0
donc j'obtiens l'équation suivante :
m²/b4-4*1/a²*( (m'+x0)/b² -1) = 0
et j'arrive donc à x0= (a²m²-4m'b²+4b4)/4b²
Or si je reprend un exemple simple et concret (http://serge.mehl.free.fr/exos/exos_gif/CerMonge1.gif )
ou je considére que ma droite d correspond a la droite PM de l'exemple avec comme équation de droite y=-1/2*x+5/2
j'obtiens x0 = 105/64 = 1.64
Je suis un peu désuvré face a ça ...
après des pages entière de calcul ...
je me suis rendu compte que je m'était trompé dans mon changement de repère !
je pense que la droite d: y=mx+m' dans le second repère donne y=mx+mx0+m' est ce exact ?
Par ailleurs je me suis trompé dans mes calculs du post précédent vu que j'avais oublié un carré dans la formule de l'ellipse !
Bref tout est faux ! :-S
je me suis rendu compte que je m'était trompé dans mon changement de repère !
je pense que la droite d: y=mx+m' dans le second repère donne y=mx+mx0+m' est ce exact ?
Par ailleurs je me suis trompé dans mes calculs du post précédent vu que j'avais oublié un carré dans la formule de l'ellipse !
Bref tout est faux ! :-S
ericswed a écrit:Je ne comprend pas ce que tu a voulu dire Black Jack :"Comme la solution de cette équation doit être double, son discriminant est nul"
Si le discriminant est nul je n aurai qu'une solution ... je n'ai pas compris ta phrase.
Plus exactement tu auras 2 solutions identiques, cela revient au même.
Il y a donc bien un seul point de contact entre l'ellipse et la droite si le discriminant de l'équation est nul ... Et c'est cela qu'on veut.
dévelloppe :
(x - Xc)²/a² + (Ax + B - Yc)²/b² = 1
b²x² + b²Xc² - 2b²x.Xc + a²A²x² + a²B² + a²Yc² + 2a²ABx - 2a²AxYc - 2a²BYc = a²b²
x²(b²+a²A²) - 2x(b²Xc - a²AB + a²AYc) + b²Xc² + a²B² + a²Yc² - 2a²BYc - a²b² = 0
Discriminant = 0 -->
(b²Xc - a²AB + a²AYc)² = (b²+a²A²).(b²Xc² + a²B² + a²Yc² - 2a²BYc - a²b²)
Tu développes le membre de gauche ...
Une volée de termes se simplifie et tu arrives à une relation du second degré en Xc
Tu peux donc alors trouver Xc (0, 1 ou 2 possibiltés différentes en fonction des valeurs de a, b , Yc, A et B).
:zen:
:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
