Bonjour !
Je suis développeur Flash et je me heurte à un probleme de mathématiques.
J'ai un menu elliptique (une ellipse de type paramétrique) qui avance d'un angle angleSpeed à chaque frame. A chaque frame, angleSpeed est divisé par 1.05, ce qui fait que l'ellipse arrete de tourner au bout d'un moment.
Ce que j'aimerais faire : à partir d'un angle donné, on détermine une distance à parcourir (angleTravel) que je connais déjà. J'aimerais déterminer quel angleSpeed donner pour obtenir un angleSpeed et un angleTravel proche de 0 au bout de n frames (= donner l'impulsion nécessaire pour que l'ellipse tourne et s'arrete aux alentours de la destination voulue).
Merci !
Ellipse et suite d'angles
7 messages
- Page 1 sur 1
Bonjour,
effectivement, il y a plusieurs angles
si l'équation cartésienne de l'ellipse est

et ses équations paramétriques (b>a)
x=a cos(t)
y=b sin(t)
t s'interpréte aisémment:
la demi-droite passant par O d'équation polaire
(angle polaire constant) coupe le cercle de centre O et de rayon R=a
en d'abscisse acos(t).
d'abscisse acos(t).
Cette demi-droite coupe un autre cercle (centre O et de rayon R=b)
en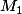 d'ordonnée b sin(t).
d'ordonnée b sin(t).
Le point M(acos(t),bsin(t)) de l'ellipse est à la croisée de leurs projections
.faire un dessin.
l'angle polaire ( )de M(x,y) sur l'ellipse est donné pour x>0
)de M(x,y) sur l'ellipse est donné pour x>0
par
=\frac{y}{x}=\frac{b}{a} tan(t))
d'où
 \tan(\frac{\pi}{2}- \theta)=\frac{a}{b}) (***)
(***)
Après , on peut faire de la trigo pour exprimer
en fonction de ?
?
ou dériver l'égalité (***) pour obtenir une relation avec les vitesses angulaires
peux tu indiquer ce que sont AngleTravel et AngleSpeed dans mes
notations ?
effectivement, il y a plusieurs angles
si l'équation cartésienne de l'ellipse est
et ses équations paramétriques (b>a)
x=a cos(t)
y=b sin(t)
t s'interpréte aisémment:
la demi-droite passant par O d'équation polaire
(angle polaire constant) coupe le cercle de centre O et de rayon R=a
en
Cette demi-droite coupe un autre cercle (centre O et de rayon R=b)
en
Le point M(acos(t),bsin(t)) de l'ellipse est à la croisée de leurs projections
.faire un dessin.
l'angle polaire (
par
d'où
Après , on peut faire de la trigo pour exprimer
en fonction de
ou dériver l'égalité (***) pour obtenir une relation avec les vitesses angulaires
peux tu indiquer ce que sont AngleTravel et AngleSpeed dans mes
notations ?
Merci pour ta réponse rapide !
En fait j'utilise l'équation paramétrique de l'ellipse pour mon code.
t correspond à angleStart sur le dessin. Il s'agit d'une ellipse avec des objets qui tournent dessus. A chaque frame, on recalcule la position de chaque objet avec l'équation de l'ellipse et une valeur t mise à jour (on ajoute angleSpeed à t). On divise également la valeur de angleSpeed par 1.05, ce qui fait qu'au bout d'un moment, t n'est plus modifié et l'ellipse s'arrete de tourner.
Ce que je cherche est la valeur de angleSpeed en fonction de angleTravel pour que l'on puisse aller de angleStart à angleEnd avec un angleSpeed et un angleTravel ( = angleStart-angleEnd) proches de 0 au bout de n frames.
PS : une frame est une image. Flash fonctionne à base d'images par secondes. A chaque image, on repasse par le code pour actualiser l'état de l'ellipse.

En fait j'utilise l'équation paramétrique de l'ellipse pour mon code.
t correspond à angleStart sur le dessin. Il s'agit d'une ellipse avec des objets qui tournent dessus. A chaque frame, on recalcule la position de chaque objet avec l'équation de l'ellipse et une valeur t mise à jour (on ajoute angleSpeed à t). On divise également la valeur de angleSpeed par 1.05, ce qui fait qu'au bout d'un moment, t n'est plus modifié et l'ellipse s'arrete de tourner.
Ce que je cherche est la valeur de angleSpeed en fonction de angleTravel pour que l'on puisse aller de angleStart à angleEnd avec un angleSpeed et un angleTravel ( = angleStart-angleEnd) proches de 0 au bout de n frames.
PS : une frame est une image. Flash fonctionne à base d'images par secondes. A chaque image, on repasse par le code pour actualiser l'état de l'ellipse.

Pour la théorie Busard-des-roseaux a parfaitement répondu et il n'y a rien à ajouter.
Pour ce qui concerne tes effets spéciaux, si tu veux suggérer un effet de freinage progressif, je te suggère, entre angle-start et angle-end d'insérer n moyens géométriques.
tn étant ta suite d'angles
tu t'arranges pour que t0=angle_start tn=angle_end.
tn+1=qtn
ll est facile de calculer q = racine-nième de angle-end/angle-start.
Tu fais des essais et tu ajustes n pour que l'effet visuel soit adéquat (pas de saccades).
Pour ce qui concerne tes effets spéciaux, si tu veux suggérer un effet de freinage progressif, je te suggère, entre angle-start et angle-end d'insérer n moyens géométriques.
tn étant ta suite d'angles
tu t'arranges pour que t0=angle_start tn=angle_end.
tn+1=qtn
ll est facile de calculer q = racine-nième de angle-end/angle-start.
Tu fais des essais et tu ajustes n pour que l'effet visuel soit adéquat (pas de saccades).
Ok, merci pour vos réponses. Malheureusement, mon niveau en maths actuellement ne dois pas dépasser celui de la seconde (voire 3e), donc ces explications m'ont semblées un peu obscures. Il me semblait qu'il fallait passer par une suite pour obtenir la valeur initiale de l'impulsion. Du coup, je vois pas trop comment interpréter vos réponses... Merci pour votre temps en tous cas !
re,
j'espère que ce n'est pas trop tard, j'avais pris quelques jours de vacances sur un autre forum :zen:
équation paramétrique de l'ellipse
x=acos(t)
y=bsin(t)
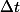 = angle speed = accroissement de la variable paramètre
= angle speed = accroissement de la variable paramètre
coordonnées polaires avec angle polaire
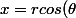)
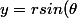)
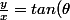=\frac{b}{a} tan(t))
si x>0
))
on calcule la dérivée de la fonction)
+b^2 sin^2(t)})
pour des petits accroissements, on confond la différentielle
avec un quotient d'accroissements finis
+b^2 sin^2(t)})
avec
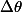 :angle travel
:angle travel
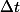 :variation de l'angle speed
:variation de l'angle speed
cos(t),sin(t): valeurs du frame précédent
Pour x<0, l'égalité différentielle est la même.
j'espère que ce n'est pas trop tard, j'avais pris quelques jours de vacances sur un autre forum :zen:
équation paramétrique de l'ellipse
x=acos(t)
y=bsin(t)
coordonnées polaires avec angle polaire
si x>0
on calcule la dérivée de la fonction
pour des petits accroissements, on confond la différentielle
avec un quotient d'accroissements finis
avec
cos(t),sin(t): valeurs du frame précédent
Pour x<0, l'égalité différentielle est la même.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
