Merci beaucoup, c'est plus compliqué que ce que je ne pensais. Quotienter A qui est déjà un quotient, ce n'est pas dans mes habitudes. J'ai du mal à visualiser
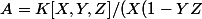))
il faut dire.
On a un premier anneau
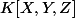
.
))
est un idéal (principal) de K. On peut donc quotienter.
On pose
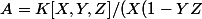))
. Les images de X, Y et Z sont x, y et z.
Par exemple,
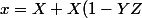 \cdot K[X, Y, Z])
, c'est l'ensemble des polynomes de K[X, Y, Z] qui, quand on les divise par
)
, il reste X. Ca existe la division euclidienne dans
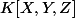
?
J'ai du mal à visualiser l'ensemble quotient. Quand je quotiente K[X] par X^2-1, j'ai un représentant de chaque classe : un polynome du premier degré, que j'obtiens en divisant par X^2-1 et en gardant le reste.
L'ensemble des polynomes de degré inférieur ou égal à 1 est un ensemble de représentants des classes d'équivalence. Et pour trouver le représentant d'un polynome, on peut diviser ou appliquer X^2=1.
Bon, ceci dit, dans Z[X], si je quotiente par (2X+1), je n'ai pas de division euclidienne...
Dans ce cas, je me dis que P et Q sont dans la même classe d'équivalence si 2X+1 divise P-Q
Du coup, 5x = x-2 car 5x-(x-2)=4x+2=2(2x+1). Mais 2x^8 = -x^7 car 2x^8 +x^7 = x^7(2x-1)
4x^8=x^5. Il suffit de retenir que 2x=-1. Mais alors x^7 n'est pas simplifiable.
En voila un drôle d'anneau, Z[X]/(2X+1). Je me demande s'il est isomorphe à un truc plus simple...
