Bonjour,
Comment chercher le Df et le Dv de la fonction : f(x) = (ln((1+x)/(1-x)))^(1/3)
Domaine de définition et de dérivabilité
5 messages
- Page 1 sur 1
Re: domaine de définition et de dérivabilité
bonjour,
il suffit de faire un tableau de signes du quotient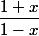
PS: sur quel domaine est définie la fonction ?
?
il suffit de faire un tableau de signes du quotient
PS: sur quel domaine est définie la fonction
Re: domaine de définition et de dérivabilité
par découpage des fonctions qui la compose :
f(x) = (ln((1+x)/(1-x)))^(1/3)
^(1/3) impose ln((1+x)/(1-x)) >=0 soit (1+x)/(1-x)>=1
ln((1+x)/(1-x)) impose (1+x)/(1-x) > 0
/(1-x) impose (1-x) non nul
finalement (1+x)/(1-x)>=1 et (1-x) non nul
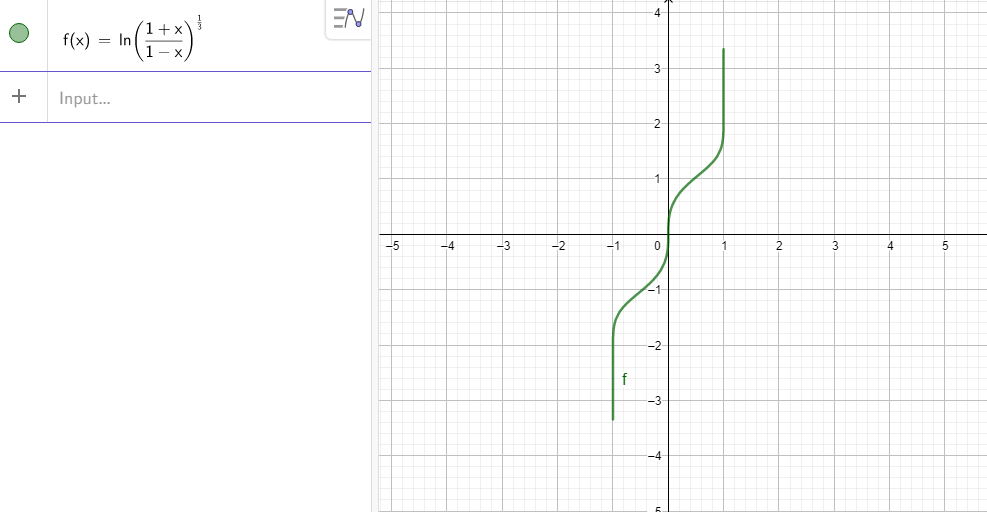
[PS] : Geogebra trouve un domaine plus large que le mien
f(x) = (ln((1+x)/(1-x)))^(1/3)
^(1/3) impose ln((1+x)/(1-x)) >=0 soit (1+x)/(1-x)>=1
ln((1+x)/(1-x)) impose (1+x)/(1-x) > 0
/(1-x) impose (1-x) non nul
finalement (1+x)/(1-x)>=1 et (1-x) non nul
[PS] : Geogebra trouve un domaine plus large que le mien
Re: domaine de définition et de dérivabilité
quel contradiction!
Qu'est-ce que je devrais faire?
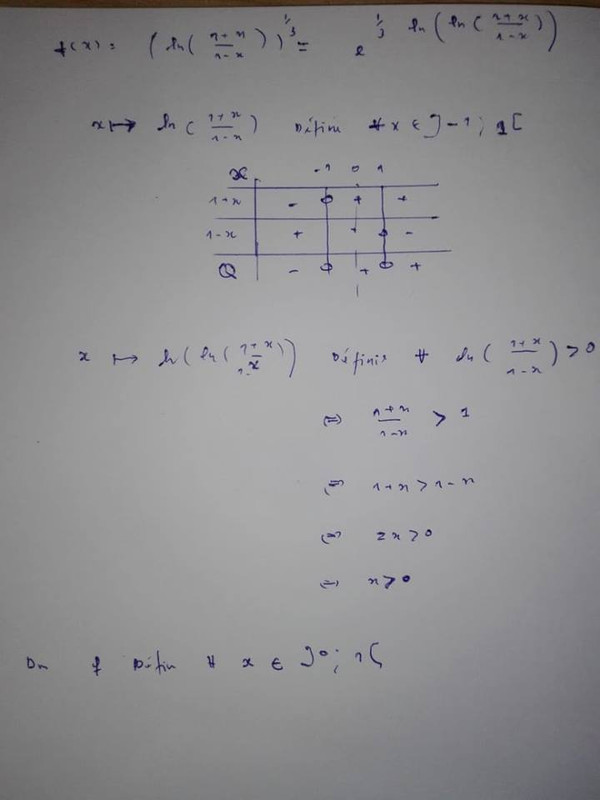

lorsque on a la racine cubique d'un reel x alors il faut que x>=0?
si oui alors la deuxieme exemple est correcte.
Qu'est-ce que je devrais faire?
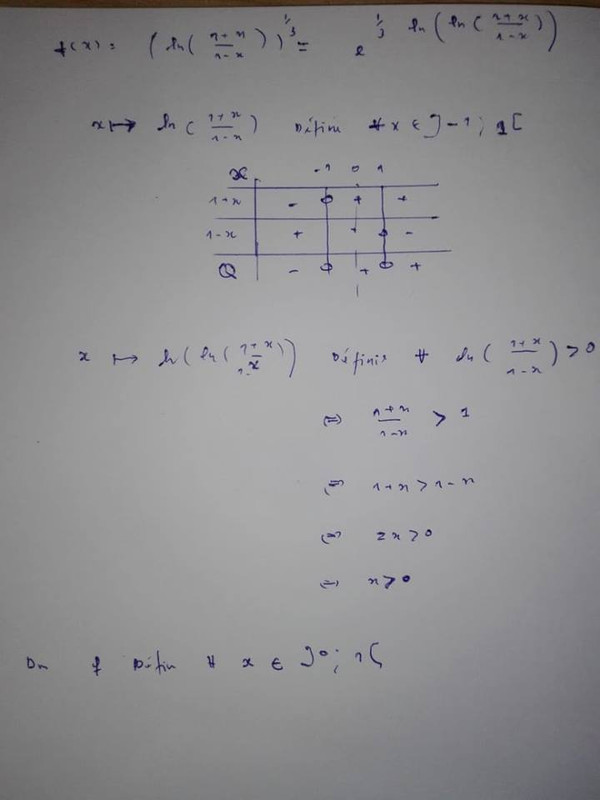


lorsque on a la racine cubique d'un reel x alors il faut que x>=0?
si oui alors la deuxieme exemple est correcte.
Re: domaine de définition et de dérivabilité
Pour moi :
la racine cubique d'un nombre négatif est "utilisable selon le contexte".
Et ceci explique la différence entre dcode ( x>=0) et géogebra.
Si je me rappelle bien, si on autorise x<0 sur avec un exposant non entier, on perd le règles de multiplication de deux puissances et on arrive à des égalités du genre -1=1
la racine cubique d'un nombre négatif est "utilisable selon le contexte".
Et ceci explique la différence entre dcode ( x>=0) et géogebra.
Si je me rappelle bien, si on autorise x<0 sur avec un exposant non entier, on perd le règles de multiplication de deux puissances et on arrive à des égalités du genre -1=1
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
