Division harmonique ??

[MacErmite]

Bonjour,

Je cherche à comprendre comment on obtient le résultat suivant :
L'auteur parle de division harmonique. Je n'ai pas trouvé de demonstration sur une division harmonique, mais directement le résultat ci-dessus.

Pour ma part je suis bloqué et trouvé ceci :

et , ce qui conduit à ...

Pouvez-vous m'aider à comprendre comment obtient-on ce résultat ?

Merci



(CI) est la normale au cercle r

[Ericovitchi]

Que les bissectrices intérieures et extérieures forment un faisceau harmonique et les relations qui vont avec, tu vas trouver des démonstrations à plein d'endroits sur le net : http://fr.wikipedia.org/wiki/Division_harmonique
Tapes "Division harmonique"

[Ben314]

Salut,
Ta méthode est bonne, mais ta formule me semble louche :
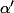
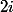
si tu apppelle et les angles en A et A' du triangle AIA' (le troisième angle étant ), tu as :

Dans ATC :
Dans A'TC :

Donc avec

mais la fraction avec des sinus ne fait pas forcément 2...

Edit : j'ai mal lu le dessin et j'ai pris le I du dessin pour le T...

[MacErmite]

Salut,
Ta méthode est bonne, mais ta formule me semble louche :
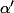
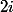
si tu apppelle et les angles en A et A' du triangle AIA' (le troisième angle étant ), tu as :

Dans ATC :
Dans A'TC :

Merci pour ta participation, cependant je n'arrive pas à te suivre je dois regarder le triangle ATC et A'TC ? Mais ce ne sont pas des triangles, je ne comprends pas :briques:

[Ben314]

Je me suis gourré : j'ai pris le I de ton dessin pour un T.

Ca devrait marcher en écrivant la loi des sinus dans ACI , A'CI (celle que j'ai donné mais avec un I et pas un T !!!) ainsi que dans TCI...

Edit : Par contre, c'est un "moins" dans la formule finale :1/CA-1/CA'=2/CT car, si le triangle AA'I est isocèle en I alors CA=CA' et CT est infini.