Dans ce qui précède, je montre quelque chose de plus fort, c'est que lorsque n est une puissance de 2, les diviseurs de 2^n+1 sont plus grand que n+1 forcément.
On peut pas adapter ceci lorsque n n'est pas une puissance de 2 car c'est faux (exemple 2^6+1 possède 5 comme diviseur).
Je crois avoir une preuve sinon.
je rappelle que je montre plutôt (c'est pareil) que si
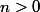
, alors
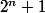
ne peut pas être divisible par

.
On sait (grâce à la décomposition en produit de facteurs premiers) que n peut s'écrire sous la forme
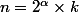
avec

,

impair.
Cherchons la forme des diviseurs premiers

de
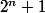
.
Soit un tel diviseur

. On a alors
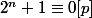
.
Alors
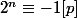
et donc
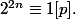
Ainsi, dans le groupe des inversibles de
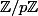
, l'ordre

de

est un diviseur de
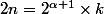
et on a
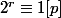
.
On sait alors que

s'écrit sous la forme
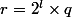
avec
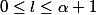
et

diviseur de

.
Si
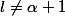
, alors

est forcément un diviseur de

et à partir de
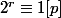
, en élevant à la puissance
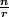
, on aboutit à
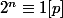
, ce qui est faux puisque
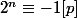
.
On en déduit alors que
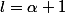
et donc
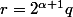
.
Comme l'ordre du groupe des inversibles de
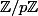
est

, on en déduit par le théorème de Lagrange que

divise

et donc qu'il existe un entier
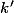
strictement positif tel que :
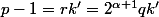
d'où
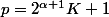
avec
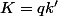
entier. Ca donne la tête des diviseurs premiers de
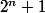
.
Si maintenant
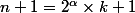
divise
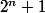
, alors

doit être un produit de diviseurs premiers de la forme décrite ci-dessus.
On voit facilement que quand on multiplie des
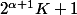
, on obtient un nombre de la même forme
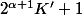
.
Et on voit facilement qu'on ne peut pas avoir
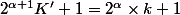
car cela implique
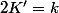
et comme k est impair...
Pseudo modifié : anciennement Trident2.