Dimension d'un sous-espace vectoriel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aston
- Messages: 6
- Enregistré le: 10 Sep 2005, 09:18
-
par aston » 23 Juil 2007, 15:01
Bonjour, voici la question demandée:
Dans l'espace vectoriel réel des fonctions de 
vers 
, quelle est la dimension du sous-espace vectoriel engendré par les cinq fonctions appliquant 
sur respectivement
, ln (2 x^2), ln (3 x^3), ln (4 x^4), ln (5x^5))
?
Justifier la réponse.Je dirais que la dimension du sous-espace est 2 puisque ces 5 fonctions sont dans le plan.
Mais comment être beaucoup plus précis ? Je n'arrive pas à trouver d'éléments théorique sur les sous-espaces vectoriels qui puissent m'aider à justifier ma réponese (si elle est correcte).
Merci.
-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
par nuage » 23 Juil 2007, 15:14
Salut,
je dirais aussi 2, mais parce que les combinaisons linéaires de ces 5 fonctions sont des combinaisons linéaires de
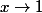
et de
.
Et que la fonction ln n'est pas constante sur
.
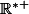
Par exemple
=\ln2 +2 \ln x)
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
par B_J » 23 Juil 2007, 15:17
salut;
=\ln(k)+k\ln(x)=\ln(k)\times 1+k\times \ln(x))
,
-
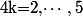
aston
- Messages: 6
- Enregistré le: 10 Sep 2005, 09:18
-
par aston » 23 Juil 2007, 15:19
nuage a écrit:Salut,
je dirais aussi 2, mais parce que les combinaisons linéaires de ces 5 fonctions sont des combinaisons linéaires de
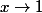
et de
.
Et que la fonction ln n'est pas constante sur
.
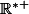
Par exemple
Ok je vois pour les combinaisons linéaire. Cependant peux-tu expliquer ce qu'est une fonction constante (non constante) et en quoi ça joue dans la justification ?
merci
-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
par nuage » 23 Juil 2007, 15:28
Une fonction constante associe à chaque valeur de la variable la même valeur.
sont des fonctions constantes.
La fonction ln n'est pas constante
)
par exemple.
Les combinaisons linéaires de fonctions constantes sont constantes, donc ln n'est pas une telle combinaison.
Ce qui assure l'indépendance linéaire de
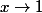
et de
dans l'espace vectoriel considéré.
La dimension du sev est donc bien égale à 2. Car il est engendré par une famille libre à 2 éléments.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
