Bonjour à tous,
j'ai du mal à concevoir la notion de différentielle intuitivement, que représente concrètement la différentielle dF d'une fonction...et en quoi elle diffère du rapport dF/dx ? Voilà, c'est assez génant de ne pas pouvoir se le représenter surtout que c'est une notion importante pour comprendre intégrale et primitive.. Je serai très content si quelqu'un pouvait éclairer ma lanterne...
Merci bp d'avance.
Différentielle
10 messages
- Page 1 sur 1
Au risque de faire hurler les vrais mathématiciens, voici une autre approche :
La différentielle est simplement un accroissement infiniment petit (= en pratique très petit)
A un accroissement de la variable dx correspond un accroissement de la fonction dF.
On montre facilement que le rapport dF/dx est simplement la dérivée de la fonction puisque :

Cette approche permet de linéariser beaucoup de problèmes
Exemple : Radiactivité.
SI on considére un intervalle de temps très petit alors le nombre de déintégrations(= la variation du nombre d'atomes qui est négative) est proportionnel au nombre d'atomes.
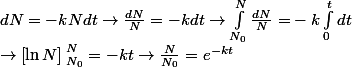
La différentielle est simplement un accroissement infiniment petit (= en pratique très petit)
A un accroissement de la variable dx correspond un accroissement de la fonction dF.
On montre facilement que le rapport dF/dx est simplement la dérivée de la fonction puisque :
Cette approche permet de linéariser beaucoup de problèmes
Exemple : Radiactivité.
SI on considére un intervalle de temps très petit alors le nombre de déintégrations(= la variation du nombre d'atomes qui est négative) est proportionnel au nombre d'atomes.
Bonsoir Izaguff:
La prémière chose que je voudrais savoir: tu études mathématiques?, si c'est vrai, tu es dans quel niveau?. Le problème est que pour les mathématiciens, la différentielle d'une application evaluée sur un point du domaine , est une transformation linéaire qui te donne las dérivées directionelles sur
, est une transformation linéaire qui te donne las dérivées directionelles sur  . (c'est la réponse qui t'a donné nuage avec la correction de yos).
. (c'est la réponse qui t'a donné nuage avec la correction de yos).
Sinon, tu cherches une autre chose. Tu peux lire quelque chose sur http://fr.wikipedia.org/wiki/Diff%C3%A9rentielle#Introduction_intuitive_des_notations_du_calcul_infinit.C3.A9simal.
À mon avis, tu cherches l'interprétation qui est utilisée par les physiciens ou les ingénieurs. L'idée d'une quantité trop petite. Si c'est comme ça, je t'acconseille de nous dire ça. Sinon, tu auras de réponses que tu ne cherches pas. Bon courage! :zen:
La prémière chose que je voudrais savoir: tu études mathématiques?, si c'est vrai, tu es dans quel niveau?. Le problème est que pour les mathématiciens, la différentielle d'une application evaluée sur un point du domaine
Sinon, tu cherches une autre chose. Tu peux lire quelque chose sur http://fr.wikipedia.org/wiki/Diff%C3%A9rentielle#Introduction_intuitive_des_notations_du_calcul_infinit.C3.A9simal.
À mon avis, tu cherches l'interprétation qui est utilisée par les physiciens ou les ingénieurs. L'idée d'une quantité trop petite. Si c'est comme ça, je t'acconseille de nous dire ça. Sinon, tu auras de réponses que tu ne cherches pas. Bon courage! :zen:
Pour une fonction dérivable de R dans R, tu as le nombre dérivé en a.
Pour une fonction différentiable de E dans F, tu as la différentielle en a : c'est pas un nombre mais une application linéaire! Cela généralise le cas précédent car le nombre dérivé f'(a) peut être vu comme une application linéaire de R dans R : x--->f'(a)x.
Cette généralisation est très déroutante (et il est normal d'être dérouté surtout au début).
Pour une fonction différentiable de E dans F, tu as la différentielle en a : c'est pas un nombre mais une application linéaire! Cela généralise le cas précédent car le nombre dérivé f'(a) peut être vu comme une application linéaire de R dans R : x--->f'(a)x.
Cette généralisation est très déroutante (et il est normal d'être dérouté surtout au début).
Bonsoir jose latino,
en fait je suis en train d'étudier les équations différentielles, je suis en PCEM1 (carré), je ne cherche donc pas dans la complication.. En fait je ne suis pas toujours à l'aise avec l'écriture différentielle. Pour commencer, je ne sais même pas exactement ce que veut dire une équation différentielle linéaire.. Notamment lors d'une équation linbéaire à variables séparables, comment se fait-il qu'on puisse écrire y' = dy/dx = f(x)/g(x) ? Quand j'étais au lycée tout celà me semblait plus facile.. Si vous pouviez m'éclairer dans un premier temps sur ce point ce serait extra..
Merci bp d'avance
en fait je suis en train d'étudier les équations différentielles, je suis en PCEM1 (carré), je ne cherche donc pas dans la complication.. En fait je ne suis pas toujours à l'aise avec l'écriture différentielle. Pour commencer, je ne sais même pas exactement ce que veut dire une équation différentielle linéaire.. Notamment lors d'une équation linbéaire à variables séparables, comment se fait-il qu'on puisse écrire y' = dy/dx = f(x)/g(x) ? Quand j'étais au lycée tout celà me semblait plus facile.. Si vous pouviez m'éclairer dans un premier temps sur ce point ce serait extra..
Merci bp d'avance
en fait pour résoudre une équation à variables séparables on doit séparer les variables certes.. Au départ on pose y'=dy/dx=f(x)/g(y) d'où on a l'écriture g(y) dy = f(x) dx. Or je ne comprend pas bien ce que celà veut dire.. J'ai d'aiileurs une question toute bête mais qui m'aiderait bien: qu'appelle - t-on variables (comment les reconnait-on) dans une équation différentielle.. Si quelqu'un pouvait m'illustrer toutes ces notions avec l'exemple de l'équation différentielle dN = k N dt (loi exponentielle) par exemple.. où sont les variables? que veut dire l'écriture y'=dy/dx=f(x)/g(y) et par conséquent l'écriture g(y) dy = f(x) dx..
Merci bp d'avance.
Merci bp d'avance.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
