Je me demande comment développer
Développement en série entière
14 messages
- Page 1 sur 1
Développement en série entière
Bonjour à tous!
Je me demande comment développer en série entière. Le développement en série de Taylor est impossible et on ne peut pas vraiment partir de
en série entière. Le développement en série de Taylor est impossible et on ne peut pas vraiment partir de  Merci!
Merci!
Je me demande comment développer
Justement, non : avec lefrankyboy1994 a écrit:D'accord je vais essayer avec les dérivées n ième, puisque je ne connais pas la formule phi de t, même si le dérivées vont rapidement se compliquer! Merci!
En plus, la formule avec un
Tu peut aussi vérifier que (heureusement), si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
frankyboy1994 a écrit:
Si je développe en série de MacLaurin, C1, c2, c3 etc. donnent zéro!
C'est justement parce que c'est plus simple avec
Sinon, effectivement, une fois que tu aura le développement de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, et même je te suggèrerais bien aussi de "poser"frankyboy1994 a écrit:Ce que tu veux dire au fond c'est qu'il faut que je pose: x^4=t et je fait les dérivations, beaucoup plus facile, avec t et ensuite je remplace les t par x^4?
ENSUITE, tu remplacera le
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ah d'accord je viens de comprendre, c'est qu'on peut écrire (1+x)^n sous la forme d'une série (le developpement du binome de Newton) et après on remplace par les valeurs de x et de n ! Mais je viens d'apprendre que mon prof a oublié d'ôter cet exercice qui n'était pas à faire lol... Mais bon merci beaucoup quand même ça m'aura appris quelque chose, de plus que je vais en actuariat à l'université, cela devrait m'être utile! Mais la formule du binome de Newton n'est elle pas seulement valide pour les nombre naturels?
frankyboy1994 a écrit:Ah d'accord je viens de comprendre, c'est qu'on peut écrire (1+x)^n sous la forme d'une série (le developpement du binome de Newton) et après on remplace par les valeurs de x et de n ! Mais je viens d'apprendre que mon prof a oublié d'ôter cet exercice qui n'était pas à faire lol... Mais bon merci beaucoup quand même ça m'aura appris quelque chose, de plus que je vais en actuariat à l'université, cela devrait m'être utile! Mais la formule du binome de Newton n'est elle pas seulement valide pour les nombre naturels?
Si, c'est pour ça qu'il te faut une "autre" formule dans le cas où \alpha n'est pas entier naturel.
En fait c'est trés simple : si tu dérive 3 ou 4 fois la fonction
Et, si
Aprés, je pense que si le prof à "enlevé" l'exo, ben c'est justement parce que vous n'avez pas vu la formule çi dessus en cours...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
frankyboy1994 a écrit:Une petite chose que je ne comprend pas encore est que les dérivées succesives de (1+x^4) et de (1+t)^alpha (dont on remplace alpha par 1/2 et t par x^4) ne sont pas les mêmes! à part ça tout est clair merci!
Ici, pour donner des noms au trucs, si on écrit
Ca veut dire qu'en fait,
Si tu dérive une fois
Par contre, si tu dérive une deuxième fois, ça commence à être "pas beau" :
On ne voit blus trés bien de lien direct entre f'' et g''. Et ça devient de pire en pire en dérivant de plus en plus (on voit de moins en moins le lien...)
Ca explique que ce soit parfaitement normal que tu ne voit pas de "lien" immédiat entre les deux.
Et ça explique aussi pourquoi je t'incitait à chercher la série entière de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour
On n'utilise pas directement l'expression de
de ) mais le fait que
mais le fait que =g(x^4)) et cette égalité reste valable pour leur DSE grâce à l'unicité de celui-ci. Si
et cette égalité reste valable pour leur DSE grâce à l'unicité de celui-ci. Si =\sum a_n x^n) , alors pour
, alors pour  ,
, 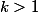 ,
, =\sum a_n x^{kn}) est encore un DSE.
est encore un DSE.
.frankyboy1994 a écrit:Ok merci BEAUCOUP! Donc c'est parce que c'est une série qu'on peut substituer le t par x^4. On ne peut évidemment par juste faire les dérivées avec t et remplacer t par x^4 dans les dérivées, c'est ce que je ne comprenais pas!
On n'utilise pas directement l'expression
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
