Salut,
J'ai une idée peut-être un poil plus élégante mais je suis pas sûr sur certains points.
L'idée serait de considérer Q comme un polynôme à coefficients dans
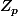
.
Le problème reviendrait donc à savoir si
}=0)
.
Considérer Q dans ce corps a deux avantages :
Avec le théorème de Wilson on a que (p-1)!=1 mod p donc on tue le
!})
.
Ensuite les dérivées successives sont très simples à calculer. Les termes en
^p)
font sortir un p quand on les dérive ce qui est très confortable puisque p=0 dans
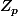
. Les dérivées successives sont donc celles de
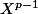
avec en facteur le reste du polynôme.
Je te laisse calculer avec ça et on trouve bien que
}=0)
.
Le point sur lequel je suis pas sûr à 100% c'est le fait de pouvoir se débarrasser aussi facilement du
!})
. Mais bon vu comme l'inverse de la classe de
!)
dans
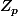
je vois pas ce qui nous en empêcherait.
Attends l'avis d'un autre pour y croire. En espérant avoir pu aider !
