Densité

[mehdi-128]

Bonsoir,

Soit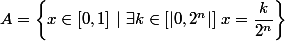

Montrer que est dense dans .

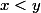
J'ai pris 2 éléments tels que . Je dois trouver un élément de compris entre et .
Mais je n'y arrive pas

[capitaine nuggets]

Salut !

Déjà qui est ?

[mehdi-128]

Salut !

Déjà qui est ?

Il n'y pas d'information sur dans l'énoncé, je suppose que c'est un entier naturel quelconque.

[LB2]

Bonjour,

est-ce que tu peux me donner un exemple d'élément de A ? et un réel de [0,1] qui n'est pas dans A?

Je propose une méthode pour la résolution :

1. Comment s'écrit un réel quelconque de [0,1] en base 2?
2. Comment s'écrit un élément de A en base 2? Que remarque-t-on?

voir par exemple : http://villemin.gerard.free.fr/NombrCar/Devpadiq.htm

[mehdi-128]

Je ne vois pas comment trouver un élément de A, le n me gêne. Je ne comprends pas c'est quoi l'ensemble vu qu'on ne connait pas .

Vous êtes sûr qu'on est obligé de passer par les bases 2 ? J'avais pensé à la propriété d'Archimède mais je n'aboutis pas trop.

[GaBuZoMeu]

Quand on a un trou de longueur et qu'on fait des pas de longueur , il y a sûrement un moment où on tombera dans le trou.

Il suffit donc d'avoir un entier naturel tel que , ou encore . Monsieur Archimède te dit qu'il en existe.

[LB2]

Je ne vois pas comment trouver un élément de A, le n me gêne. Je ne comprends pas c'est quoi l'ensemble vu qu'on ne connait pas .

Vous êtes sûr qu'on est obligé de passer par les bases 2 ? J'avais pensé à la propriété d'Archimède mais je n'aboutis pas trop.

1. Il manque un quantificateur "il existe" devant n
2. Non, on n'est absolument pas obligé de passer par LA base 2 (cf post de GBZM)
En revanche, ma méthode peut être utile pour essayer de comprendre de quoi on parle avec cet ensemble A, et donc de donner du sens à la question.
Attention, si tu veux résoudre le problème avant de comprendre l'énoncé, cela rappelle la devise shadok : Quand on ne sait pas où on va, il faut y aller… Et le plus vite possible

[mehdi-128]

Quand on a un trou de longueur et qu'on fait des pas de longueur , il y a sûrement un moment où on tombera dans le trou.

Il suffit donc d'avoir un entier naturel tel que , ou encore . Monsieur Archimède te dit qu'il en existe.

On peut obtenir cette condition avec Archimède ...

Mais comment savez vous que c'est cette condition qu'il fallait poser ?

[mehdi-128]

Je ne vois pas comment trouver un élément de A, le n me gêne. Je ne comprends pas c'est quoi l'ensemble vu qu'on ne connait pas .

Vous êtes sûr qu'on est obligé de passer par les bases 2 ? J'avais pensé à la propriété d'Archimède mais je n'aboutis pas trop.

1. Il manque un quantificateur "il existe" devant n
2. Non, on n'est absolument pas obligé de passer par LA base 2 (cf post de GBZM)
En revanche, ma méthode peut être utile pour essayer de comprendre de quoi on parle avec cet ensemble A, et donc de donner du sens à la question.
Attention, si tu veux résoudre le problème avant de comprendre l'énoncé, cela rappelle la devise shadok : Quand on ne sait pas où on va, il faut y aller… Et le plus vite possible

Je ne comprends déjà rien à l'exercice alors la base 2 ça va être encore pire surtout que je ne vois pas le rapport.

[GaBuZoMeu]

Mais comment savez vous que c'est cette condition qu'il fallait poser ?

Tu n'as pas lu les deux premières lignes de mon message ?

[alb12]

salut,
avec notre questionneur, il convient d'etre patient https://www.ilemaths.net/sujet-partie-dense-821425-2.html

[Tuvasbien]

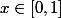
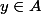
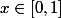
Dire que est dense dans c'est dire que pour tout , pour tout , il existe tel que . On considère le segment que l'on découpe en segments avec arbitraire que l'on choisira avantageusement plus tard. On a . Si , alors il est dans l'un de ces intervalles : il existe tel que . Comment choisir un élément de assez proche de et pour avoir ?

[LB2]

Pour comprendre les propos de Tuvasbien et GBZM, il convient de faire un dessin du découpage du segment [0,1] en l'union des [(k-1)/2^n, k/2^n] pour n=1, n=2, n=3 ...

[mehdi-128]

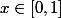
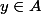
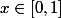
Dire que est dense dans c'est dire que pour tout , pour tout , il existe tel que . On considère le segment que l'on découpe en segments avec arbitraire que l'on choisira avantageusement plus tard. On a . Si , alors il est dans l'un de ces intervalles : il existe tel que . Comment choisir un élément de assez proche de et pour avoir ?

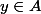
Merci j'ai compris tout le début mais le point qui me pose problème est de déterminer un élément tel que ...
J'ai fait des dessins mais je ne vois pas.

[GaBuZoMeu]

Tu n'as toujours rien compris ou rien lu des deux premières lignes de mon message plus faut.
Le trou, c'est l'intervalle entre et . Quelle est la longueur du trou ?
Si tu fais des pas de longueur strictement plus petite que la longueur du trou, alors à un moment tu vas tomber dans le trou. Tu comprends ça ?

[mehdi-128]

"Quand on a un trou de longueur et qu'on fait des pas de longueur , il y a sûrement un moment où on tombera dans le trou."
La longueur du trou c'est .
Un pas correspond à quoi ici ?
La longueur des pas c'est quoi ?
Et le il correspond à quoi dans votre analogie ?

[Tuvasbien]

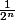
Ce sont des pas de longueur , concernant mon message, si alors un élément de proche de est ou (il y avait pas trop le choix...), si par exemple on pose alors alors comment choisir pour avoir ? Au fond c’est la même idée que GaBuZoMeu mais rédigée différemment.

[mehdi-128]

@Tuvabien

Je comprends mieux avec votre méthode

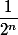
Oui j'avais compris que est un élément des bornes du segment . La longueur de cet intervalle étant , on a bien

Mais on veut avoir donc on choisit tel que :

Ce qui donne : soit par croissance de la fonction ln.

Enfin :

C'est juste ? Ça m'a l'air bizarre le moins

[GaBuZoMeu]

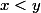
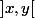
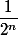
Soient tel que . L'intervalle est un trou de longueur . Choisissons entier naturel suffisamment grand pour que la longueur du pas soit strictement plus petite que la longueur du trou .
On fait tous les pas qu'on peut pour arriver jusqu'au trou : soit le plus grand entier tel que . Au pas d'après, on est dans le trou : .

[mehdi-128]

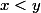
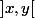
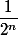
Soient tel que . L'intervalle est un trou de longueur . Choisissons entier naturel suffisamment grand pour que la longueur du pas soit strictement plus petite que la longueur du trou .
On fait tous les pas qu'on peut pour arriver jusqu'au trou : soit le plus grand entier tel que . Au pas d'après, on est dans le trou : .

Joli et expliqué de façon super simple et accessible, en faisant un dessin j'ai compris direct. Merci

Est-il utile de justifier l'existence du

Je dirais que contient 0 donc elle est non vide. C'est aussi une partie de majorée par donc elle admet un plus grand élément.