Bonjour (ou bonsoir ?),
On considère les vecteurs V à N composantes dont les valeurs sont prises dans E={1, 2, ..., K).
On suppose N>=K.
Combien y en a-t-il satisfaisant à la condition « contenir au moins une fois chaque élément de E » ?
J'avais d'abord pensé à une formule comme
arrangements(N,K)*K^(N-K)
mais elle compte plusieurs fois certains vecteurs et puis on voit facilement qu'elle est fausse, par exemple pour K=1.
En effet elle donne N alors qu'il n'y a qu'un vecteur possible (à savoir (1,1,1..., 1)).
C'est sans doute un problème classique de dénombrement, mais mes cours de maths sont bien loin.
Merci d'avance pour toute idée constructive
Dénombrement de vecteurs entiers
6 messages
- Page 1 sur 1
Re: Dénombrement de vecteurs entiers
Je réfléchis tout haut.
Déjà, combien y a-t-il en tout de façons de mettre N objets dans K boites (... c'est un peu plus simple exprimé ainsi)
Il y a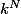 façons.
façons.
Parmi toutes ces dispositions , combien occupent au maximum j boites (avec j<= k) ?
Combien occupent uniquement les boites 1,2, 3... j :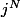
Mais ici, j'ai imposé les boites 1 à j , mais il y a plein de façons de choisir j boites parmi les N ... donc en tout :
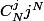
Ca doit être faux ... parce que les distributions qui occupent moins de j boites sont comptées plusieurs fois dans ce calcul.
Et là, pour corriger ça, il faut faire intervenir le crible de Poincaré.
Voilà le mot clé qui devrait t'aider à avancer.
Là, je suis parti sur la piste : les distributions qui occupent les k boites, ce sont toutes les distributions, sauf celles qui n'occupent pas toutes les boites.
Il y a peut-être d'autres pistes.
Déjà, combien y a-t-il en tout de façons de mettre N objets dans K boites (... c'est un peu plus simple exprimé ainsi)
Il y a
Parmi toutes ces dispositions , combien occupent au maximum j boites (avec j<= k) ?
Combien occupent uniquement les boites 1,2, 3... j :
Mais ici, j'ai imposé les boites 1 à j , mais il y a plein de façons de choisir j boites parmi les N ... donc en tout :
Ca doit être faux ... parce que les distributions qui occupent moins de j boites sont comptées plusieurs fois dans ce calcul.
Et là, pour corriger ça, il faut faire intervenir le crible de Poincaré.
Voilà le mot clé qui devrait t'aider à avancer.
Là, je suis parti sur la piste : les distributions qui occupent les k boites, ce sont toutes les distributions, sauf celles qui n'occupent pas toutes les boites.
Il y a peut-être d'autres pistes.
Re: Dénombrement de vecteurs entiers
Un vecteur doit comprendre les chiffres 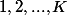
et les dispositions possibles sur les composantes forment un ensemble
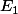 , de taille
, de taille =A\begin{pmatrix}<br />N\\ <br />K<br />\end{pmatrix}) . Un élément de
. Un élément de 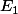 peut être vu comme un vecteur
peut être vu comme un vecteur 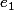 de dimension
de dimension  avec
avec 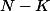 composantes nulles.
composantes nulles.
Ces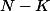 chiffres « libres »sont à choisir dans
chiffres « libres »sont à choisir dans 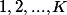 .
.
Pour eux, l'ensemble des dispositions est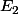 avec
avec = K^{N-K}) .
.
On est donc tenté de dire que le nombre cherché est simplement le
produitcard(E_{2})) .
.
Mais on peut décrire un élément de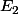 comme un vecteur
comme un vecteur 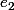 de
de
dimension , avec
, avec  composantes nulles.
composantes nulles.
Pour construire l'ensemble cherché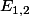 on prend toutes les paires d'éléments
on prend toutes les paires d'éléments ) et l'on construit le vecteur
et l'on construit le vecteur 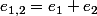 .
.
Le problème est que cela crée des doublons. Et il ne s'agit pas d'une union au sens classique et la formule du crible de Poincaré ne s'applique pas. On notera d'ailleurs que l'intersection de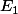 et
et 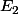 est vide.
est vide.
et les dispositions possibles sur les composantes forment un ensemble
Ces
Pour eux, l'ensemble des dispositions est
On est donc tenté de dire que le nombre cherché est simplement le
produit
Mais on peut décrire un élément de
dimension
Pour construire l'ensemble cherché
Le problème est que cela crée des doublons. Et il ne s'agit pas d'une union au sens classique et la formule du crible de Poincaré ne s'applique pas. On notera d'ailleurs que l'intersection de
Re: Dénombrement de vecteurs entiers
Il manque un mot important vers la fin de mon dernier message :
« Pour construire l'ensemble cherché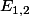 on prend toutes les paires d'éléments
on prend toutes les paires d'éléments ) orthogonaux ...»
orthogonaux ...»
« Pour construire l'ensemble cherché
Re: Dénombrement de vecteurs entiers
Salut,
En fait, ton truc est plus connu sous l'intitulé du "nombre de surjections d'un ensemble à N éléments dans un ensemble à K éléments".
Et le résultat, c'est :
=\sum_{q=1}^K (-1)^{K-q}{K \choose q} q^N)
Et il y a plusieurs méthodes classiques pour le montrer dont la méthode du crible ou bien par récurrence en utilisant le fait évident (pourquoi ?) que :
)
En fait, ton truc est plus connu sous l'intitulé du "nombre de surjections d'un ensemble à N éléments dans un ensemble à K éléments".
Et le résultat, c'est :
Et il y a plusieurs méthodes classiques pour le montrer dont la méthode du crible ou bien par récurrence en utilisant le fait évident (pourquoi ?) que :
Modifié en dernier par Ben314 le 05 Déc 2021, 11:32, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Dénombrement de vecteurs entiers
Merci, je me doutais bien que c'était un problème connu et résolu.
Personnellement, je suis plus à l'aise avec la démonstration par récurrence.
Personnellement, je suis plus à l'aise avec la démonstration par récurrence.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
