Démonstration par récurrence

[Sunatory]

Bonjour,
Je cherche à démontrer par récurrence n^2>=n! pour tout n>=4
Pourriez vous me guider s'il vous plaît ?

[infernaleur]

4²=16
4!=24
Donc c'est faux

[Sunatory]

n^2<=n! pardon je me suis trompé de sens

[infernaleur]

à toi de continuer

[Sunatory]

Je pense avoir compris un certain raisonnement mais certains aspects me bloquent tout de même..
Merci pour la rapidité de réponse !

[Pseuda]

Bonjour,

Initialisation :
La proposition est vraie pour n=4 : 16<=24.

Hérédité :
Supposons qu'elle est vraie au rang n : n^2 <= n !.
Montrons qu'elle est vraie au rang n+1 :
(n+1)^2 = (n+1)*(n+1) <= (n+1)*n^2 (pour utiliser l'hypothèse de récurrence) <= (n+1)*n ! = (n+1) !

Il n'y a qu'une seule étape à justifier, c'est n+1 <= n^2 pour n>=4 (car ....). C'est évident, mais il faut bricoler une démonstration je te laisse la faire.

[zygomatique]

salut

je me fous de l'initialisation

ce qui m'intéresse c'est l'hérédité car visiblement une récurrence s'impose ...

on suppose donc que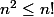 pour un certain n



la propriété est donc héréditaire pour n >= 3

or (initialisation ...)

donc ...

[Ben314]

Salut,
Perso., je suis pas bien convaincu de la pertinence de l'outil "récurrence" dans un cas pareil.
Certes, on peut prendre comme définition de la factorielle le fait que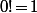 et 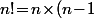qui conduit inévitablement à faire une récurrence (vu qu'on a une définition par récurrence...)
Mais on peut aussi partir de la simple définition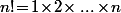 qui implique que lorsqu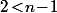e (i.e. 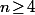) puis vérifier que lorsque .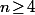
On peut évidement aussi partir de (pour 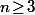) puis résoudre .

Enfin, bon, on peut évidement faire une récurrence parce que c'est ce qui est demandé, mais celui qui a demandé de faire une preuve par récurrence aurait sans doute mieux fait de réfléchir un peu plus afin de donner un exemple plus pertinent d'utilisation de l'outil "récurrence"...

[Pseuda]

Bonjour Ben314,

Certains profs n'hésitent pas à faire démontrer 2n>=n par récurrence... Je trouve ça idiot aussi.