Démonstration par récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 16:12
par typhlon » 16 Sep 2007, 16:12
Bonjour,
je cherche depuis un certain nombre d'heure à montrer par récurrence la validité de:
n(d indice(n)+d indice(n-1) = (n+1)d indice (n)+(-1)^(n+1).
Merci à ceux qui prendront la peine de me répondre.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 16:40
par fahr451 » 16 Sep 2007, 16:40
bonjour
qui est d ?
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 16:45
par typhlon » 16 Sep 2007, 16:45
d indice n, est une suite. pourquoi?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 16:48
par fahr451 » 16 Sep 2007, 16:48
n 'importe laquelle ?...
alors je prends la suite nulle et je te dis faux ...
ça devient vraiment pénible toutes ces demandes d'aide avec des énoncés erronés
 par legeniedesalpages » 16 Sep 2007, 16:49
par legeniedesalpages » 16 Sep 2007, 16:49
Bonjour, il faudrait en savoir plus sur la suite
_{n\in \mathbb{N})
, car cette égalité est fausse en général.
Par exemple si on prend la suite nulle
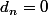
, pour tout entier n, cette suite ne vérifient pas l'égalité.
grillé par fahr

-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 16:50
par typhlon » 16 Sep 2007, 16:50
je suis vraiment désolée pour le manque de précision mais je n'ai que ça et n'étant pas tout à faite experte en la matière je ne peux pas te dire mieux.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 16:53
par fahr451 » 16 Sep 2007, 16:53
alors tu écris
FAUX
en rouge sur ta feuille et tu ajoutes il suffit de considérer la suite nulle
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 16:55
par typhlon » 16 Sep 2007, 16:55
je peux juste vous dire que cette suite n'est pas nulle admettant pour d indice 0=1 et d indice 1=0
 par legeniedesalpages » 16 Sep 2007, 16:59
par legeniedesalpages » 16 Sep 2007, 16:59
typhlon a écrit:je peux juste vous dire que cette suite n'est pas nulle admettant pour d indice 0=1 et d indice 1=0
il faut connaitre quand meme les autres
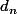
, à part si c est une suite de deux éléments ??
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 17:14
par typhlon » 16 Sep 2007, 17:14
je peux bien calculer les autres par moi même ou tout au moins une partie et ils ne me sont pas nécessaires pour établir ma récurrence
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 17:20
par typhlon » 16 Sep 2007, 17:20
oui, je sais que d indice (n+1)=(n+1)d indice (n)+(-1)^(n+1)
une solution?
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 17:39
par typhlon » 16 Sep 2007, 17:39
la relation n'a pas aidé?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 17:41
par fahr451 » 16 Sep 2007, 17:41
typhlon a écrit:oui, je sais que d indice (n+1)=(n+1)d indice (n)+(-1)^(n+1)
une solution?
hum hum
il faudrait savoir
cette relation est elle celle que tu as par hypothèse ou celle que tu voudrais démontrer ?
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 17:46
par typhlon » 16 Sep 2007, 17:46
la relation que je veux démontrer, sachant que l'égalité que j'ai inscrite lors de mon premier post est tirée du fait que les 2 parties de l'équation correspondent chacune à d indice (n+1)...Donc je suppose qu'il serait plus logique de tenter de démontrer la première que j'ai demandé...
 par legeniedesalpages » 16 Sep 2007, 17:46
par legeniedesalpages » 16 Sep 2007, 17:46
Tu nous as posté a tout début:
typhlon a écrit:Bonjour,
je cherche depuis un certain nombre d'heure à montrer par récurrence la validité de:
n(d indice(n)+d indice(n-1) = (n+1)d indice (n)+(-1)^(n+1).
Merci à ceux qui prendront la peine de me répondre.
maintenant tu nous dit que la suite
)
est définie par la relation de récurrence:
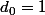
et
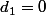
,
pour tout entier

,
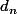
est défini tel que :
(d_{n-1}+d_{n-2}) = n d_{n-1}+(-1)^n)
.
Que cherches-tu à montrer avec cette suite?
Edit: désolé j'avais pas vu les derniers posts.
 par legeniedesalpages » 16 Sep 2007, 17:52
par legeniedesalpages » 16 Sep 2007, 17:52
peut-être dois-tu montrer que la suite
)
est bien définie, c'est à dire que pour tout entier

, il existe un unique réel

tel que
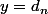
.
-
typhlon
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Sep 2007, 17:35
-
 par typhlon » 16 Sep 2007, 18:11
par typhlon » 16 Sep 2007, 18:11
franchement je sais plus trop, je suis un peu perdue je dois l'avouer. Quoi qu'il en soit, merci beaucoup pour votre aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
) est définie par la relation de récurrence:
est définie par la relation de récurrence: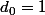 et
et 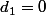 ,
,  ,
, 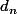 est défini tel que :
est défini tel que :(d_{n-1}+d_{n-2}) = n d_{n-1}+(-1)^n) .
.