Démonstration par récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aston
- Messages: 6
- Enregistré le: 10 Sep 2005, 09:18
-
par aston » 24 Déc 2006, 13:40
Bonjour,
Je voudrais savoir si mon raisonnement de ma démonstration est correct.
Voici l'énoncer:
 = \frac{n(n+1)(n+2)}{3})
--------------------------
(n+2)}{3} = \frac{(n^2 + n)(n+2)}{3})
(n+2)}{3} = \frac{n^3 + 3n^2 + 2n}{3})
(1)
Voici ma démonstration:
pour n =1:
2 =
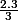
---> OK
pour n+1:
 + (n+1)(n+2) = \frac{(n+1)(n+2)(n+3)}{3})
(n+3)}{3})
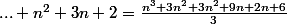
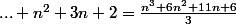
 = n^2 + 3n + 2)
On remarque dès lors que après la soustraction ci-dessus on a une égalité avec la dernière partie du membre de gauche juste avant. CQFD
Je ne sais pas si c'est très clair et surtout si c'est mathématiquement (logiquement) correct.
Merci d'avance.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 24 Déc 2006, 13:44
Pas du tout correct.
Tu confonds hypothèse et conclusion.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
par fahr451 » 24 Déc 2006, 13:45
une remarque pourquoi développer pour refactoriser ensuite alors qu'on peut factoriser directement par(n+1)(n+2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
