Corps commutatifs et anneaux de fractions

[matheuxendetresse]

Salut,

J'ai cet exo, et je sais pas comment le commencer.
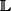
Soient et des corps commutatifs.
on veut savoir si la proposition suivante est vraie ou fausse:


Niveau: L2

[Ben314]

Salut,
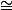
Je suppose que le symbole que tu utilise signifie "isomorphe", mais isomorphe en temps que quoi ?
Je suppose que c'est en temps qu'anneau (commutatif unitaire), mais une certitude serait appréciée . . .

[hdci]

Bonjur,

Une idée qui me vient (sans avoir approfondi) : si les deux espaces de polynômes sont isomorphes, alors l'isomorphisme envoie les polynômes constants de l'un sur ceux de l'autre ; cela pourrait suffire ?

[matheuxendetresse]

Salut,
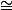
Je suppose que le symbole que tu utilise signifie "isomorphe", mais isomorphe en temps que quoi ?
Je suppose que c'est en temps qu'anneau (commutatif unitaire), mais une certitude serait appréciée . . .

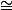
Oui par le symbole je veux dire isomorphes, le premier comme anneaux commutatifs unitaires et le deuxièmes comme corps commutatifs.

[Ben314]

Dans l'anneau , les éléments non nuls de sont caractérisés par le fait qu'ils divisent tout les autres :

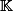
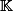
Et ça prouve que ton isomorphisme (d'anneau) de sur envoie les éléments de sur ceux de et donc réalise un isomorphisme d'anneaux unitaire de sur (qui est forcément un isomorphisme de corps).

[matheuxendetresse]

Bonjur,

Une idée qui me vient (sans avoir approfondi) : si les deux espaces de polynômes sont isomorphes, alors l'isomorphisme envoie les polynômes constants de l'un sur ceux de l'autre ; cela pourrait suffire ?

Ah oui, alors si comme je considère que qui est isomorphe à

Merci bien.

[matheuxendetresse]

Dans l'anneau , les éléments non nuls de sont caractérisés par le fait qu'ils divisent tout les autres :

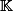
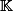
Et ça prouve que ton isomorphisme (d'anneau) de sur envoie les éléments de sur ceux de et donc réalise un isomorphisme d'anneaux unitaire de sur (qui est forcément un isomorphisme de corps).

Merci beaucoup : )

[Ben314]

Par contre, je sais pas si c'est vrai pour des anneaux (commutatifs unitaires mais pas forcément intègre, histoire de pas avoir accès au corps des fraction) :

[matheuxendetresse]

Par contre, je sais pas si c'est vrai pour des anneaux (commutatifs unitaires mais pas forcément intègre, histoire de pas avoir accès au corps des fraction) :

Oui, parce que l'on s'appuie sur le fait que l'anneau soit intègre pour définir à partir de
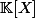
Merci

[Ben314]

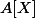
C'est pas uniquement ça le problème : Si (anneau commutatif, unitaire, intègre) alors le morphisme d'anneau de sur défini par est évidement un isomorphisme, mais il n'envoie pas sur .

[matheuxendetresse]

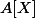
C'est pas uniquement ça le problème : Si (anneau commutatif, unitaire, intègre) alors le morphisme d'anneau de sur défini par est évidement un isomorphisme, mais il n'envoie pas sur .

Ah oui, je vois.
Merci

[tournesol]

Ne pourrait on pas utiliser l'injection canonique i:k donne (k,0,0,...)
et la surjection canonique s:(l0,l1,l2,.....) donne l0
puis si f désigne l'isomorphisme, considérer r o f o i ?

[matheuxendetresse]

Ne pourrait on pas utiliser l'injection canonique i:k donne (k,0,0,...)
et la surjection canonique s:(l0,l1,l2,.....) donne l0
puis si f désigne l'isomorphisme, considérer r o f o i ?

Pardon, j'ai pas trop bien compris, tu peux expliciter?
merci

[Ben314]

Ne pourrait on pas utiliser l'injection canonique i:k donne (k,0,0,...)
et la surjection canonique s:(l0,l1,l2,.....) donne l0
puis si f désigne l'isomorphisme, considérer r o f o i ?

Si ce dont tu parle c'est de l'injection et de la surjection alors dans le cas où est l'isomorphisme de mon précédent message, on a ça :

qui ne fourni pas du tout un isomorphisme de sur .