Contre exemple théorème de Cesaro

par **bitonio** » 01 Oct 2006, 16:30

Bonjour,

Je n'arrive pas à trouver un contre exemple pour une réciproque:

soit

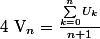
propriété à démontrer: si

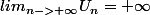
, alors

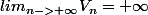
J'ai réussi sans problème à démontrer cette propriété. Mais je dois démontrer que la réciproque est fausse: je cherche donc une fonction

qui ne tend pas vers

qui donne une fonction

qui tend vers

merci d'avance pour un contre exemple !

CIaoo

par **anima** » 01 Oct 2006, 16:37

Oubliez :--:

par **tize** » 01 Oct 2006, 16:40

tu dois prendre une suite

qui n'est pas monotone ...

par **Quidam** » 01 Oct 2006, 16:45

anima a écrit:Ca me semble évident a démontrer. La somme d'une suite de terme tous tendant vers l'infini tend vers l'infini aussi. Mais le contre-exemple pour la réciproque:

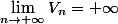
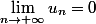
Cependant, est tout aussi vrai, du moment que la limite est asymptotique. Apres tout, tu ajoute des trucs; le résultat augmente, mais de peu. Ce qui fait que ta suite tend toujours vers +infini, sans pour autant que tous les termes de ta suite tendent vers cela...

Ce que tu dis n'est pas clair !

1 - D'abord il ne s'agit pas d'une "somme d'une suite de terme tous tendant vers l'infini". Dire que tous les termes d'une suite Un tend vers l'infini n'a pas de sens ! Même chose pour "sans pour autant que tous les termes de ta suite tendent vers cela" !
2 - En outre, il ne s'agit pas d'une somme mais d'une moyenne...Et je pense que le problème est entièrement différent !

3 - La phrase "Mais le contre-exemple pour la réciproque:

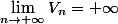
" n'a pas de verbe et je ne parviens pas à "deviner" ce que tu as voulu dire !

par **xon** » 01 Oct 2006, 16:46

Salut,

je crois que la suite qui vaut n si n est pair et 0 sinon marche

par **anima** » 01 Oct 2006, 16:47

Quidam a écrit:Ce que tu dis n'est pas clair !

1 - D'abord il ne s'agit pas d'une "somme d'une suite de terme tous tendant vers l'infini". Dire que tous les termes d'une suite Un tend vers l'infini n'a pas de sens ! Même chose pour "sans pour autant que tous les termes de ta suite tendent vers cela" !
2 - En outre, il ne s'agit pas d'une somme mais d'une moyenne...Et je pense que le problème est entièrement différent !

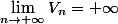
3 - La phrase "Mais le contre-exemple pour la réciproque: " n'a pas de verbe et je ne parviens pas à "deviner" ce que tu as voulu dire !

Je ne suis jamais clair

et oui, j'ai mal lu. Ne tiens pas compte du post. Oublie le :mur:

par **bitonio** » 01 Oct 2006, 16:49

xon a écrit:Salut,

je crois que la suite qui vaut n si n est pair et 0 sinon marche

effectivement

par **Quidam** » 01 Oct 2006, 16:50

Je propose la suite

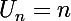
si n est pair,

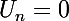
sinon. Alors

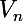
tend vers l'infini (enfin, je crois) et certainement pas

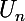
Qu'en penses-tu Bitonio ?

par **Quidam** » 01 Oct 2006, 16:51

xon a écrit:Salut,

je crois que la suite qui vaut n si n est pair et 0 sinon marche

Oooops ! Désolé ! Tu as gagné !

par **Quidam** » 01 Oct 2006, 16:52

anima a écrit:Je ne suis jamais clair et oui, j'ai mal lu. Ne tiens pas compte du post. Oublie le :mur:

Oublier, d'accord ! Mais oublier quoi ? :ptdr:

par **bitonio** » 01 Oct 2006, 16:54

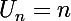
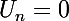
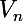
Quidam a écrit:Je propose la suite si n est pair, sinon. Alors tend vers l'infini (enfin, je crois) et certainement pas
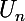
Qu'en penses-tu Bitonio ?

Il est clair que Un n'a ici pas de limite... par contre la somme des Un est égal à (n+1)(n)/2 à quelque chose près... donc ca marche... j'ai bien compris ?

par **xon** » 01 Oct 2006, 16:55

oui c'est bien çà :we:

par **bitonio** » 01 Oct 2006, 16:57

et pour rédiger je m'en sors comment ? :marteau:

il suffit de dire que

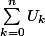
est environ égal à

?

Y'a pas un peu mieux ?

EDIT: d'ailleur c'est faux cette pseudo égalité non ?

par **xon** » 01 Oct 2006, 17:02

tu peux calculer exactement la somme en remarquant que çà revient à faire la somme des nombres pairs cette somme se calculant en mettant 2 en facteur et en remarquant que tu retrouves la somme des E(n/2) premiers nombres.

par **bitonio** » 01 Oct 2006, 17:19

j'essaye, merci pour la piste :++:

par **bitonio** » 01 Oct 2006, 18:22

parfait, mille mercis !

Contre exemple théorème de Cesaro

Contre exemple théorème de Cesaro

Qui est en ligne