Bonjour j'aimerais trouver des contre-exemples qui montreraient que cet ensembe :
{f, l f l continue en 0} avec f une fonction de R dans R n'est pas un sous-espace vectoriel.
merci de votre réponse
Cordialement
Science
Contre-exemple espace vectoriel
6 messages
- Page 1 sur 1
Pour ton contre exemple tu peut peut prenre une fonction discontinue telle que f(x)=-f(-x) (la valeur absolue sera donc continue en zéro) et une fonction constante.
La valeur absolue de leur somme n'est clairement pas continue en zéro.
De même l'espace
E=f tel que |f| derivable en zero n'est pas un espace vectoriel, j'explique
en gros, une fonction verra sa valeur absloues continue en zéro si elle même ne change pas de signe en 0.
Si tu prend=x^{2}) on a bien
on a bien 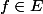 de même pour
de même pour =e^{x}) .
.
Bon maintenant f-g change de signe en zero, on a donc un point d'inflexion et la fonction n'est pas dérivable.
La valeur absolue de leur somme n'est clairement pas continue en zéro.
De même l'espace
E=f tel que |f| derivable en zero n'est pas un espace vectoriel, j'explique
en gros, une fonction verra sa valeur absloues continue en zéro si elle même ne change pas de signe en 0.
Si tu prend
Bon maintenant f-g change de signe en zero, on a donc un point d'inflexion et la fonction n'est pas dérivable.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
