Contournement de Riemann

[Restefond34]

Bonjour,

Je bloque sur un point de l'exercice suivant.
L'objectif de l'exercice est de calculer l'intégrale I par deux méthodes. J'ai réussi celle où on fait deux petits changements de variables.
Sur la seconde, on doit passer par une sorte de "discrétisation" de l'intégrale. Une fois qu'on a le produit, j'ai réussi à le calculer en utilisant des relations coefficient-racine et je retombe sur la même valeur qu'en utilisant le changement de variable (ouf^^)

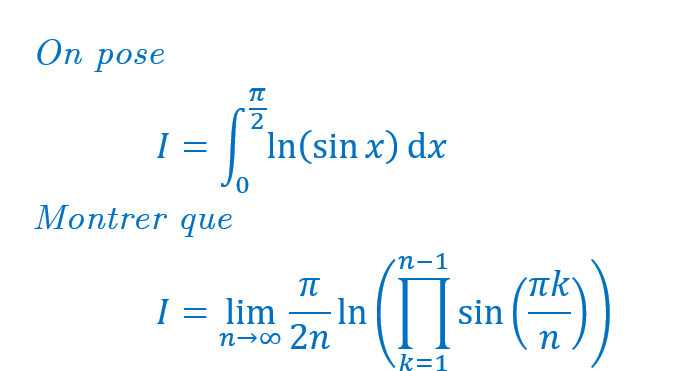
Le problème est pour justifier le passage de l'intégrale au produit. Ca ressemble énormément à une somme de Riemann, mais je n'arrive pas à la justifier car ici, la fonction x -> ln(sin(x)) n'est pas continue en 0. Je me suis dit qu'on pouvait peut-être poser un epsilon>0 et scinder l'intégrale sur [0,epsilon] et [epsilon, pi/2] mais il va y avoir des problèmes d'interversion de limites...

Auriez-vous une idée ?

Merci et bonne journée !

[GaBuZoMeu]

N'y a-t-il pas une erreur dans la formule, allant de 0 à tandis que va jusqu'à ?

[Restefond34]

Oui, en effet, I est une intégrale qui va jusqu'à pi.
J'ai confondu car j'ai montré auparavant que l'intégrale de 0 à pi valait le double de l'intégrale de 0 à pi/2

[GaBuZoMeu]

Je m'intéresse plutôt à



Vu que la fonction est croissante sur , on peut encadrer cette somme d'aires de rectangles entre deux intégrales de (de bornes pas forcément et ). Ensuite, on fait tendre vers l'infini.

Bon, après si tu tiens à avoir , on peut toujours utiliser .

[Restefond34]

Bonjour,

Je vous remercie pour votre réponse.
En faisant votre choix, j'obtiens ainsi ceci :



Là, j'ai envie de dire que chacune des deux bornes tend vers . Pour le justifier, je dirais que cela découle du fait que cette intégrale existe effectivement et comme les deux bornes des suites d'intégrales tendent vers 0 et pi/2, je suis ramené à la définition de l'intégrabilité. Cela semble correct ?

Le problème, c'est qu'une fois que j'ai pu dire cela, le calcul du produit des sin(kpi/2n) pour k=1 à k=n-1 me pose problème. Pour celui des sin(kpi/n) de k=1 à k=n-1, ça se passait bien (avec des racines de polynômes). Mais là, même en utilisant la duplication du sinus, ça me ramène à un nouveau produit de cos(kpi/2n) que je ne sais pas mieux gérer... Ou alors je m'embrouille ?

[GaBuZoMeu]

Pourquoi prends tu la somme de 2 à et pas de 1 à ???? L'intégrale (généralisée) de 0 à est bien inférieure à , non ?

Tu as un problème avec les cosinus ? Mais , n'est-ce pas ?

[Restefond34]

Effectivement, de k=1 à k=n-1, cela marche bien, autant pour moi

Pour le produit, moi celui que j'ai calculé, c'est .
Or, ici, avec votre méthode, j'ai besoin de .
Mais
=
=
=

Et j'obtiens alors ce que je cherche ?
Visiblement, en terminant le calcul, je retombe bien sur la baleur -ln(2)/2, c'est formidable !

[Kolis]

Bonsoir !
On peut utiliser les sommes de Riemann lorsqu'on a une intégrale convergente (avec bornes finies) dès que la fonction à intégrer est monotone sur des voisinages des bornes. Bien entendu on doit tronquer les sommations pour éviter des termes non définis dans la somme.