Changement d'indice prepa ECS

[oceanevp]

Je ne comprends pas comment on réalise les changements d'indices lorsque l'on a 2K, ce sont 2 exemples qui illustrent ce que je ne comprends pas dans la démarche...
Si quelqu'un peut m'aider svp

[Ben314]

Salut,
Ben visiblement, c'est le B-A-BA de l'utilisation du symbole qui t'a un peu échappé : quand on écrit , ça veut dire qu'on fait la somme des 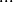pour toutes les valeurs entières de k allant de 1 à n.

Ensuite, si tu "pose" j=2k-1
- Déjà, lorsque k va varier de 1 à n, alors j va varier de 2x1-1=1 à 2n-1 et surement pas de 1 à .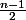
- Ensuite, je vois absolument pas ce que vient f... ton inégalité dans l'histoire : quand on te demande combien vaut la somme des trois premiers nombres d'une série, est-ce que, sous prétexte que , tu pense que cette somme sera forcément la même que celle des cinq premier nombre de la série ? (parce que là, c'est exactement ce que tu affirme...)
- Enfin, comme "changement de variable", c'est n'importe quoi : si k prend les valeurs successives 1,2,3,4 alors j=2k-1 prend les valeurs 1,3,5,7 et tu voit bien que ce ne sont pas toutes les valeur entières de 1 à 7 (sans compter le fait que de 1 à 4, il y a 4 valeurs alors que de 1 à 7, il y en a 7...)

[oceanevp]

Donc pour le premier exemple, je sépare ma somme en 2 cas avec k pair et k impair :
- pour k impair, je fais mon changement d'indice j: 2k-1 et j'ai la somme pour K allant de 1 à 2n+1 de J
- pour k impair je fais aussi un changement d'in

[Razes]

Pourquoi tu ne sépare pas la somme en deux parties, ça serait plus simple. Non?

[Ben314]

Ben non, tu t'en fout complètement de savoir si k est pair ou pas. Le truc qui est forcément impair (que k soit pair ou pas), c'est j=2k-1.
Donc si tu tenais absolument à "poser" j=2k-1, ce qu'il faudrait écrire, c'est un truc du style .
Sauf que déjà, la somme de droite, c'est pas trop "conventionnel" comme écriture (mais à peu prés tout le monde comprend ce que ça veut dire) et ensuite, c'est pas forcément super pratique à utiliser.

A la limite, on pourrait continuer dans la foulée en écrivant que :


Mais a mon sens, c'est vraiment chercher la m... que de procéder ainsi alors qu'on pouvait bêtement écrire que

[oceanevp]

Merci vraiment de votre aide, c'est vrai que c'est chercher la m.. alors qu'on peut procéder beaucoup plus simplement mais merci d'avoir pris la peine de m'expliquer. Une dernière faveur comment procédez-vous pour passer de la somme de K pour K allant de 1 à 2n-1 (k pair donc on pose K=2j) à la somme de j allant de 1 à n-1. Je ne comprends pas comment fonctionne le changement des ''indices'' comme le montre mon exemple 2

[Ben314]

Les nombre pairs entre 1 et 2n-1 (compris), c'est 2, 4 , 6 , ... , 2n-2 (le suivant, à savoir 2n est trop grand)
C'et à dire 2x1 , 2x2 , 2x3 , ... , 2(n-1) donc c'est tout les nombres de la forme 2j avec j entre 1 et n-1 (compris).

Sinon, de façon un peu plus générale, tant que c'est pas super clair (et pour le moment ça semble pas trop l'être...) je t'inciterais fortement à récrire au brouillon les différents trucs contenant des symboles sigma (et/ou les indices sur lesquels on somme) sous la forme de somme avec des points de suspension (et/ou de suites de nombres entiers séparés par des virgules).
Par ce que, au fond, c'est jamais que ça qu'on manipule et que ça permet au début de mieux comprendre le "pourquoi du comment" on a le droit de faire tel ou tel truc.
Par exemple, j'ai vu certains étudiant se demander pourquoi on avait le droit d'écrire que alors que, écrit sous la forme ils voient tous que ce n'est pas un "nouveau théorème" mais une façon un peu différente d'écrire un truc connu depuis le collège...

[Ben314]

Et pour revenir par exemple à ça :
- A gauche du égal, c'est "la somme de tout les truc de la forme 2k-1 où k est un entier entre 1 et n (inclus)", c'est à dire (2*1-1) + (2*2-1) + (2*3-1) + ... + (2n-1)
- A droite du égal, c'est "la somme de tout les entiers impairs compris entre 1 et 2n-1 (inclus)", c'est à dire 1+3+5+...+(2n-1)

Et vu sous cette forme, c'est on ne peut plus clairement la même chose (et ça donne pas mal l'impression que, en passant de l'un à l'autre, on n'a pas vraiment fait "avancer le schmilblick"....)

[oceanevp]

Je viens à peine de voir votre message, merci infiniment cela me parait beaucoup plus clair !