DM de Maths sur Polynômes prépa ECS

[grehwmuty]

Bonjour à toutes et à tous ;)
Un ami qui vous fréquente régulièrement m'a conseillé de venir plancher sur quelques exos de terminales, premières ou classes inférieures.
Mais je viens ici pour une toute autre cause en réalité : ça fait 45 minutes que je suis sur un DM de Maths (je suis en prépa ECS) et rien à faire, je ne trouve pas la première question qui est capitale pour la suite.

Voici l'énoncé :

Pour quelle valeur du paramètre réel N l'équation suivante (E) :

N P(X) - (2X + 1) P'(X) - (X²+X) P''(X) = 0

a t elle une solution polynomiale non nulle de degré n?

Pour cette valeur de N, démontrer qu'il existe un unique polynôme Pn de degré n tel que Pn(0)=1.

J'ai donc transformé mes polynômes en somme, j'ai regroupé les sommes en factorisant par X^k mais j'arrive à une énorme ligne de calcul improbable avec des sommes = 0. Ainsi je ne peux résoudre.

Auriez vous une petite astuce? :mur:

Merci d'avance ;)

[busard_des_roseaux]

Bjr,

au départ, j'ai cherché à annuler le coefficient constant dans le membre
de gauche de l'égalité. Puis le coeff du monome de degré 1.

Finalement, on remarque que l'application


est un endomorphisme (linéaire) de l'espace vectoriel des polynômes de degré 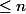, ceci quelque soit n,
et le problème revient à chercher un polynôme du noyau de de degré n.

Mais, on peut choisir une base de ,
soit la base canonique ,soit une famille bien choisie (des polynomes d'interpolation de Lagrange, des polynômes de Bernstein,
tout ce qui forme un drapeau ...)

dans cette base , f_n a une matrice.
Et ptêt que l'on peut démontrer cela par récurrence sur l'entier n.

désolé de ne pas pouvoir t'en dire plus.

[XENSECP]

Ah un ECS
Alala, la réponse a été claire je pense non ?

[busard_des_roseaux]

finalement,

supposons que l'équation admette une solution polynomiale S
de degré n.

S s'écrit
où Q est un polynôme de degré au plus (n-1).

On peut supposer S polynome unitaire.

En composant par f (linéaire)



f(Q) est un polynôme de degré au plus (n-1).

La coordonnée de sur est

d'où la condition nécessaire

[busard_des_roseaux]

On note , par abus de langage, la restriction de f à avec N=n(n+1)


La matrice de f est "presque" diagonale
les éléments diagonaux sont



on calcule le déterminant de cette matrice.

comme la suite est injective, ou disons strictement croissante, la restriction de f à chaque E_k est bijective (déterminant non nul)
pour k <n.


Il y a donc un vecteur non nul dans le noyau de f qui n'est pas dans le
noyau de pour tout k <n.

PS: quelles sont les références de l'énoncé ?

[grehwmuty]

Oula (A)

J'ai bien relu vos messages et j'ai franchement du mal à comprendre (je regarde même mon cours sur les espaces vectoriels, j'en suis arrêté à "Espace Vectoriel, Sous espace vectoriel". (je n'ai pas fait les matrices).

Mais je pense que le DM porte sur les "polynômes".

Ainsi j'ai remplacé "P" par Somme de 0 à n des a(indice k) X^k. Pour P' j'obtiens une forme comme celle-ci et pareil pour P".

Ensuite j'ai regroupé et j'ai trouvé des p'tites résidus (lol) et un grand polynôme en regroupant les sommes des .....X^k.

Or un polynôme est nul si et seulement si ses b(indice k) sont nuls.

Donc j'obtiens ce système :

a(indice n) (N-3n+n²)=0
a(indice 1) (N-4) - 2 a(indice 2) = 0
a (indice k) (N-2k-2k²) - (k+1) a(indice k+1) = 0 (avec k=2,...,n-1)
Na(indice 0) - 3a(indice 1) = 0

Mais de là, je ne sais pas trop quoi faire. Ici, je pense qu'il faut modéliser la condition "une solution polynomiale de degré n" mais j'avoue que je suis dans l'impasse...

:marteau: