jankyjack a écrit:je vous remercie de votre reponse mais je ne comprends plus à partir de là où vous dites que (t, Theta, h) va balayer un petit parallélépipède rectangle de coté dr * dtheta * dh.
Ce que j'ai écrit, c'est que :
LORSQUE (t, Theta, h) va balayer un petit parallélépipède rectangle de coté dr * dtheta * dh alors blablabla...
Donc jusque là, il n'y a rien à "comprendre", je vais regarder
ensuite ce qu'il se passe pour (x,y,z)
lorsque (t, Theta, h) décrit se parallélépipède.
Et ce qui se passe, c'est l'approximation affine des fonctions (i.e. leur développement de Taylors à l'ordre 1) qui le donne : pour
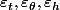
"petits" on a
 \cr<br />y(t\!+\!\varepsilon_t,\theta\!+\!\varepsilon_\theta,h\!+\!\varepsilon_h) \cr<br />z(t\!+\!\varepsilon_t,\theta\!+\!\varepsilon_\theta,h\!+\!\varepsilon_h) \cr<br />\end{pmatrix}<br />\approx <br />\begin{pmatrix} <br />x(t,\theta,h)\cr<br />y(t,\theta,h)\cr<br />z(t,\theta,h)<br />\end{pmatrix}<br />+\begin{pmatrix} <br />\frac{\partial x}{\partial t}(t,\theta,h) \cr<br />\frac{\partial y}{\partial t}(t,\theta,h) \cr<br />\frac{\partial z}{\partial t}(t,\theta,h)<br />\end{pmatrix}\varepsilon_t<br />+\begin{pmatrix} <br />\frac{\partial x}{\partial \theta}(t,\theta,h) \cr<br />\frac{\partial y}{\partial \theta}(t,\theta,h) \cr<br />\frac{\partial z}{\partial \theta}(t,\theta,h)<br />\end{pmatrix}\varepsilon_\theta<br />+\begin{pmatrix} <br />\frac{\partial x}{\partial h}(t,\theta,h) \cr<br />\frac{\partial y}{\partial h}(t,\theta,h) \cr<br />\frac{\partial z}{\partial h}(t,\theta,h)<br />\end{pmatrix}\varepsilon_h)
Ce qui signifie que, lorsque
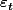
décrit
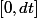
;
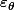
décrit
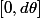
et
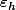
décrit
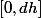
, c'est à dire lorsque le point
)
décrit un petit parallélépipède rectangle de volume
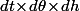
alors pendant ce temps là, le point
\,;\,<br />y(t\!+\!\varepsilon_t,\theta\!+\!\varepsilon_\theta,h\!+\!\varepsilon_h)\,;\,<br />z(t\!+\!\varepsilon_t,\theta\!+\!\varepsilon_\theta,h\!+\!\varepsilon_h)\Big))
décrit (approximativement) un parallélépipède (non rectangle) porté par les vecteurs
 \cr<br />\frac{\partial y}{\partial t}(t,\theta,h) \cr<br />\frac{\partial z}{\partial t}(t,\theta,h)<br />\end{pmatrix}dt\ ;\ <br />\begin{pmatrix} <br />\frac{\partial x}{\partial \theta}(t,\theta,h) \cr<br />\frac{\partial y}{\partial \theta}(t,\theta,h) \cr<br />\frac{\partial z}{\partial \theta}(t,\theta,h)<br />\end{pmatrix}d\theta<br />\text{ et }<br />\begin{pmatrix} <br />\frac{\partial x}{\partial h}(t,\theta,h) \cr<br />\frac{\partial y}{\partial h}(t,\theta,h) \cr<br />\frac{\partial z}{\partial h}(t,\theta,h)<br />\end{pmatrix}dh)
Et ce parallélépipède à pour volume
 &<br />\frac{\partial x}{\partial \theta}(t,\theta,h) &<br />\frac{\partial x}{\partial h}(t,\theta,h) \cr<br />\frac{\partial y}{\partial t}(t,\theta,h) &<br />\frac{\partial y}{\partial \theta}(t,\theta,h) &<br />\frac{\partial y}{\partial h}(t,\theta,h) \cr<br />\frac{\partial z}{\partial t}(t,\theta,h) &<br />\frac{\partial z}{\partial \theta}(t,\theta,h) &<br />\frac{\partial z}{\partial h}(t,\theta,h) \cr<br />\end{pmatrix}\right|\!\times\!dt\!\times\!d\theta\!\times\!dh)
