[PrépaECE] Bloqué sur une intégrale.

[Plimpton]

Si si, tu peux l'écrire ! Je l'ai vu écrit sous cette forme (avec le sigma) dans plusieurs livres, etc. D'ailleurs, une expérience non aboutie avait était faite à propos de la conductivité d'un courant électrique entre deux plaques séparées par du vide, et cette somme égale à -1/12 a permis de débloquer les calculs, et les résultats trouvés étaient justes. C'est aussi une formule utilisée dans la théorie des cordes. Cela dit, je pense personnellement que ce n'est pas vraiment une complète "égalité", il faudrait peut-être un autre symbole mathématique pour représenter ça, mais en tout cas par le calcul, on peut aboutir à l'infini tout comme à -1/12.

[Robot]

On peut bien sûr écrire n'importe quoi. De là à prétendre que ce qu'on écrit est toujours vrai ...

[Skullkid]

C'est donc reparti pour le casse-tête, je vais être un peu rèche du coup.

NON, on ne peut pas écrire rigoureusement que la somme des entiers est égale à -1/12, c'est faux et très facile à démontrer. C'est un abus de langage extrêmement grossier qui persiste parce que la formule écrite tel quel est impressionante, surtout pour le lecteur qui n'y connaît rien. Quand on la voit écrite par quelqu'un avec un vrai bagage mathématique et de l'honnêteté intellectuelle, elle est inmanquablement précédée d'une foule d'avertissements qui insistent sur le fait qu'on est en train de vulgariser des concepts mathématiques compliqués, et qu'il ne faut pas tout prendre pour argent comptant (avertissements que les lecteurs se font souvent une joie d'ignorer, comme tu l'as visiblement fait).

Il est tout à fait rigoureux de dire que , il est tout à fait rigoureux de dire que est la somme des puissances -s des entiers non nuls lorsque Re(s) > 1, et il est tout à fait rigoureux de dire que la régularisation par 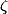assigne la valeur -1/12 à la série des entiers naturels. Toutes ces phrases ont un sens mathématique précis et sont correctes. Aucune d'elles ne dit que la somme des entiers naturels est égale à -1/12. Et j'insiste : on est en train de parler d'énoncés mathématiques démontrables et démontrés, il n'y a pas de "je pense personnellement que" qui tienne. On ne te demande pas ton avis.

C'est très bien de se renseigner en lisant de la vulgarisation scientifique, mais faut arrêter de croire que la vulgarisation remplace la connaissance. C'est pas mal énervant de voir des gens débarquer de nulle part et sortir des trucs hallucinants et grossièrement faux sur un sujet scientifique à la mode parce qu'ils ont vu un reportage de 10 minutes au 20 heures de TF1 (bouuuh les protons de Fukushima qui brûlent et qui font une bombe atomique !). Je suis à fond pour la vulgarisation scientifique (bien faite, évidemment) et je m'oppose régulièrement à des gens qui pensent qu'il faudrait absolument réserver le discours scientifique à une élite à cause du risque de mécompréhension (y a d'ailleurs eu une discussion y a pas si longtemps sur le forum où je prenais le parti d'un vulgarisateur qui a écrit sur le sujet), donc ça m'attriste d'autant plus de lire ce genre de posts qui tend à leur donner raison...

L'expérience physique dont tu parles est la mise en évidence de l'effet Casimir, qui est lié à une force qui s'éxerce entre deux plaques conductrices, ce qui n'est pas du tout la même chose que "la conductivité d'un courant électrique entre deux plaques" (ce qui ne veut rien dire d'ailleurs). Encore une fois, je trouve ça super de voir un élève de lycée assez curieux pour s'intéresser à l'effet Casimir, à la théorie des cordes et à la fonction zêta, mais c'est nettement moins ravissant de voir le même élève se poser en expert de sujets qu'il ne comprend pas (et c'est normal, ce sont des sujets compliqués) et suggérer d'aller se renseigner à des gens capables de faire la différence entre ce qu'ils savent et ce qu'ils ignorent.

En un mot comme en cent,

[center][/center]

[Plimpton]

donne-nous les valeurs de a, b et c

[Plimpton]

salut ! Dans certains cas, la boucle for peut être remplacée par une somme (notée par un sigma majuscule) ou par un produit (pi majuscule)
Par exemple, dans ce cas-la, c'est possible :

Pour i allant de 1 à 9
S prend la valeur 1/i
M prend la valeur M+S
Fin-pour

Ce qui peut être représenté par la somme pour i allant de 1 à 9 de 1/i.
Par contre, ça marche pas si tu utilise la boucle For comme suite récurrente, comme dans ce cas la :

Pour i allant de 1 à 9
S prend la valeur S*i
Fin-pour
Fin-pour

[Plimpton]

Il suffit d'étudier la fonction log[base 3] (2^x-5)

[Lostounet]

Ouais mais qu'est-ce que tu veux faire avec ?

[Plimpton]

Voir quand ça marche avec x et y entiers ... Ouai c'est dur en fait

[lulu math discovering]

:ptdr: l'illustration...

Mais ça m'intéresse beaucoup tout ça. Quelle est la différence mathématique entre ce que tu dis et "la somme de tous les entiers est -1/12" ?

Pardon si la différence est évidente et que je ne l'ai pas vue.

[Sylviel]

La différence entre l'une des trois phrases suivantes :
-
- est la somme des puissances -s des entiers non nuls lorsque Re(s) > 1
- la régularisation par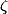 assigne la valeur -1/12 à la série des entiers naturels.

et "la somme de tous les entiers est -1/12"

Je te laisse lire...

Dans le premier cas on parle d'une fonction, pas d'une somme,
dans le second on dis qu'une fonction est une somme pour des s de partie réelle strictement supérieure à 1 (donc certainement pas pour -1 qui est le cas correspondant à "la somme de tous les entiers")
dans le troisième il y a les termes "régularisation par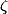 " en plus.

[lulu math discovering]

- Je ne connais pas la fonction donc... désolé de ne pas comprendre le premier argument. :hum:
- OK je retiendrais, on n'est en dehors de la définition de la fonction puisqu'ici Re(s)<1 :zen:
- kézako la régularisation ? :hein:

[Sylviel]

tu poses la question "quelle est la différence", je te l'ai explicité. Je n'ai pas prétendu expliquer les différents termes (cf. les posts précédent pour cela).

[Plimpton]

Pour le 2), -1.34 fonctionne non ?

[lulu math discovering]

Beuuh, mais y en a compliqué... (un kikoo déçu)

[Lostounet]

Je trouve personnellement plus enrichissant mathématiquement, enfin pour moi, d'étudier la fonction zêta là où ça va bien plutôt que de faire en (-1) sans maitriser les bases :ptdr:
C'est déjà un bon exercice.

[Plimpton]

Hey mec, tu sais que la partie de 0 à 1 est la plus importante de toutes ? Pourtant la fonction Zeta de base est définie sur Re(s)>1

[Lostounet]

Pour un jour pouvoir comprendre les choses compliquées faisant intervenir la fonction Zêta, pourquoi ne pas maitriser ça avant? :

http://www.maths-france.fr/MathSpe/GrandsClassiquesDeConcours/SeriesDeFonctions/FonctionZetaDeRiemann.pdf

[Sake]

Pour un jour pouvoir comprendre les choses compliquées faisant intervenir la fonction Zêta, pourquoi ne pas maitriser ça avant? :

http://www.maths-france.fr/MathSpe/GrandsClassiquesDeConcours/SeriesDeFonctions/FonctionZetaDeRiemann.pdf

Et encore, là, il s'agit de la fonction zêta de Riemann réelle...

[Lostounet]

Oui voilà.
Déjà tu (Plimpton) vois comme c'est "tordu" (pas forcément difficile...) de trouver les propriétés de base de la fonction Zeta sur R (sens de variation, limites, quelques valeurs particulières). Enfin c'est juste mon avis...

[lulu math discovering]

Merci beaucoup pour le lien !!