[MPSI] Bloqué sur un petit exo sur l'orthogonalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 18 Mai 2007, 17:57
par pouik » 18 Mai 2007, 17:57
Bonsoir,
pourriez-vous m'aider à résoudre cet exercice sur lequel je n'arrive pas à partir. Merci d'avance.
Soient

un espace euclidien et
.)
Montrer l'équivalence entre :
1.

conserve l'orthogonalité, i.e. :
 \in R^2)
,

est orthogonal à

implique
)
est orthogonal à
)
.
2. il existe
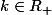
tel que :
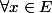
,
|| = k||x||.)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Mai 2007, 18:31
par fahr451 » 18 Mai 2007, 18:31
bonsoir
1=>2
prendre une bon (e1,...,en) les images sont orthogonales
et comme ei+ej est orthogonal à ei-ej à ei +ej ( j et i différents) on voit que les normes des f(ei) sont toutes égales
2=>1 k non nul f /k linéaire conserve la norme donc le produit scalaire donc l'orthogonalité
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 18 Mai 2007, 19:02
par pouik » 18 Mai 2007, 19:02
Merci,
mais pourriez-vous détailler un peu plus la première implication, je ne comprends pas très bien !
merci d'avance.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Mai 2007, 19:35
par fahr451 » 18 Mai 2007, 19:35
ei orthogonal à ej donc f (ei) à f(ej)
ei+ej orthogonal à ei-ej donc
f(ei) +f(ej) à f( ei) - f(ej) ce qui donne en faisant le produit scalaire
ll f(ei)ll^2 = ll f(ej)ll^2 donc égalité des normes on note k cette norme commune
pour x quelconque
on a x = sigma xi ei avec llxll^2 = sigma xi^2
f(x) = sigma xi f (ei)
ll f(x))ll^2 = sigma xi^2 ll f(ei)ll^2 car les f(ei) orthogonaux
soit ll f(x)ll^2 = k^2 sigma xi^2 = k^2 ll xll^2
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 18 Mai 2007, 19:38
par kazeriahm » 18 Mai 2007, 19:38
tu sais surement que tu peux trouver une base orthonormée de E, notée (e1,...,en)
comme l'as dit fahr, tu peux vérifier que ei+ej est orthogonal à ei-ej (car ||ei||=1)
donc f(ei+ej)|f(ei-ej)=0, ce qui te donne par othogonalité de f(ei) et de f(ej), ||f(ei)||=||f(ej)||, et ce pour tout i et j.
Alors soit k=||f(ei)||, regarde ce qui se passe ensuite pour x quelconque, en décomposant x sur ta base (e1,...,en)
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 18 Mai 2007, 19:39
par kazeriahm » 18 Mai 2007, 19:39
:we: ah bon trop tard
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 18 Mai 2007, 21:45
par yos » 18 Mai 2007, 21:45
Une base n'est pas indispensable je dirais :
conservation de l'orthogonalité entraîne conservation des rapports de longueurs (comme l'a fait Fahr :
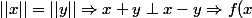+f(y)\perp f(x)-f(y)\Rightarrow ||f(x)||=||f(y)||)
).
Et ça donne bien une similitude.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Mai 2007, 21:49
par fahr451 » 18 Mai 2007, 21:49
absolument
j'ai failli passer par Eij mais je me suis retenu )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités