Bijection de Q vers R (ou N)

[tartus]

Bonjour,

J'ai deux questions :

1. Y a t'il une bijection de vers ?
2. Y a t'il une bijection de vers ?

Merci d'avance

[ffpower]

1. Non
2. Oui

:happy2:

[Ben314]

1. Non
2. Oui

:happy2:

Tu pourrait dire bonjour quand même :zen:

[benekire2]

Salut !

Puisque FF fais le gentil et donne les réponse ( bon, ok , ça n'a aucune valeur mais ça permet de vérifier .. ) je propose des preuves :

Bon, on va montrer la deuxième d'abord : Que dire de l'application qui àassocie ?

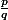
Ensuite montre plusieurs choses :
- Un ensemble est dénombrable ssi il possède une suite exhaustive de parties finies.
- Le produit cartésien de deux ensembles dénombrables est dénombrable

Bien, sûr c'est pas dur de montrer que Z est dénombrable ( au pire , [-n,n] est une suite exhaustive de parties finies ... )

Pour la non dénombrabilité de R, on fera ça après, mais l'idée de la preuve me semble-il est de construire une bijection entre P(N) l'ensemble des parties de N et R puis d'utiliser le Théorème de Cantor.

PS. Pour une preuve sous forme d'exo niveau TS , proposé par Nightmare (bijection entre N et Q) : http://www.maths-forum.com/kholle-cancres-105311.php