Une bijection de ]a,b[ vers R
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 11 Nov 2006, 19:26
par aviateurpilot » 11 Nov 2006, 19:26
trouver une bijection de
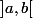
vers

-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 11 Nov 2006, 19:36
par Zebulon » 11 Nov 2006, 19:36
Bonsoir,
il suffit de se rapporter à l'intervalle

et d'utiliser tangente.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 19:37
par yos » 11 Nov 2006, 19:37
Avec une fct affine, tu envoies ]a,b[ vers ]-pi/2, pi/2[ et ensuite tu prends la fct tangente. La composée de ces deux fonctions convient.
amusant aussi :trouver une bijection de [0,1] sur [0,1[
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 11 Nov 2006, 19:40
par simplet » 11 Nov 2006, 19:40
yos a écrit:amusant aussi :trouver une bijection de [0,1] sur [0,1[
en effet c'est marrant... je reflechis... :hum:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 11 Nov 2006, 19:48
par Zebulon » 11 Nov 2006, 19:48
yos a écrit:trouver une bijection de [0,1] sur [0,1[
Il faut chercher une limite de suite de fonctions ?
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 11 Nov 2006, 19:54
par simplet » 11 Nov 2006, 19:54
est-ce qu'il faut "passer" de [0,1] sur un autre intervalle pour "revenir" à [0,1[ , ou on peut trouver directement la fonction bijective??
et si tu n'avais pas formuler la question de cette facon j'aurai dit que ces deux intervalles n'étaient pas en bijection :-)) :triste:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 11 Nov 2006, 20:02
par Zebulon » 11 Nov 2006, 20:02
Si tu passes par un autre intervalle, il faudra quand même montrer une fois qu'on peut passer "bijectivement" d'un intervalle fermé à un intervalle semi-fermé.
Je pensais plutôt à ça :
=\lim\limits_{n\to +\infty}f_n(x))
avec, pour tout
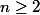
,
=x-{x\over n})
.
Alors chaque

est définie sur [0,1] à valeurs dans

et est bijective. Peut-on en déduire que f est à valeurs dans [0,1[ et est bijective ?
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 11 Nov 2006, 20:08
par simplet » 11 Nov 2006, 20:08
Moi aussi j'avais penser à ca. MAis 0 n'est pas atteint. Ah bah si j'ss bete!! non, moi en fait j'av pris x -> x+1/n voila pourquoi..
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 11 Nov 2006, 20:08
par Zebulon » 11 Nov 2006, 20:08
simplet a écrit:MAis 0 n'est pas atteint.
Si ! Pour tout
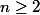
,
=0)
!
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 11 Nov 2006, 20:09
par simplet » 11 Nov 2006, 20:09
g modifié mon post juste avant :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 20:12
par yos » 11 Nov 2006, 20:12
Ces deux intervalles sont en bijection car ils ont tous les deux la puissance du continu.
Il ne faut bien sûr pas chercher dans les fonctions continues.
L'exemple de zebulon est une fct continue car la limite est x ---> x non?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 11 Nov 2006, 20:15
par Zebulon » 11 Nov 2006, 20:15
Ce qui m'embête, c'est plutôt que, si on définit f comme ça,
=\lim\limits_{n\to +\infty}(1-{1\over n})=1)
...
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 11 Nov 2006, 20:20
par Zebulon » 11 Nov 2006, 20:20
yos a écrit:Ces deux intervalles sont en bijection car ils ont tous les deux la puissance du continu.
D'accord, mais comment montre-t-on qu'ils ont la puissance du continu autrement qu'en montrant qu'ils sont chacun en bijection avec

, et donc en explicitant chaque bijection, ce qui donnera, par composée, une bijection entre les deux ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 11 Nov 2006, 20:41
par alben » 11 Nov 2006, 20:41
Bonsoir
Je pense qu'il faut faire un traitement particulier pour les rationnels contenus dans [0,1]. Ils sont dénombrables et on doit pouvoir les mettre en bijection avec N
De même les rationnels contenus dans [0,1[ sont aussi dénombrables, donc en bijection avec N et donc aussi avec ceux contenus dans [0,1]. Pour les réels non rationnels, l'identité doit marcher
Ca semble pouvoir tenir la route mais je ne suis pas sur :triste:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 21:05
par yos » 11 Nov 2006, 21:05
Zebulon a écrit:D'accord, mais comment montre-t-on qu'ils ont la puissance du continu autrement qu'en montrant qu'ils sont chacun en bijection avec

, et donc en explicitant chaque bijection, ce qui donnera, par composée, une bijection entre les deux ?
Tu me surprends!
Il n'y a qu'un élément d'écart entre ces deux ensembles infinis...
De toute façon c'est évident que tout intervalle non vide a la puissance du continu.
L'idée d'Alben est bonne. On peut même se limiter aux éléments 1/k de [0,1] (k entier) . A ceux là on fait un traitement spécial, et aux autres encore plus simple.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 11 Nov 2006, 21:14
par alben » 11 Nov 2006, 21:14
yos a écrit:On peut même se limiter aux éléments 1/k de [0,1] (k entier) . A ceux là on fait un traitement spécial, et aux autres encore plus simple.
Oh oui, joli :king2:
C'est l'hôtel de Hilbert !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 21:17
par yos » 11 Nov 2006, 21:17
alben a écrit:C'est l'hôtel de Hilbert !
c'est quoi ça?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 11 Nov 2006, 21:21
par alben » 11 Nov 2006, 21:21
yos a écrit:c'est quoi ça?
un classique On n'utilise ici que la première partie
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 21:30
par yos » 11 Nov 2006, 21:30
Merci pour le lien. Je faisais de l'hotel de Hilbert sans le savoir.
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 11 Nov 2006, 21:44
par B_J » 11 Nov 2006, 21:44
Salut ;
la fonction definie par :
f(x)=1/(n+2) si x=1/n , n entier naturel non nul
f(x)=1/2 si x=0
et f(x) = x sinon
repond a la question
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
=\lim\limits_{n\to +\infty}f_n(x)) avec, pour tout
avec, pour tout 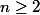 ,
, =x-{x\over n}) .
. est définie sur [0,1] à valeurs dans
est définie sur [0,1] à valeurs dans  et est bijective. Peut-on en déduire que f est à valeurs dans [0,1[ et est bijective ?
et est bijective. Peut-on en déduire que f est à valeurs dans [0,1[ et est bijective ?, et donc en explicitant chaque bijection, ce qui donnera, par composée, une bijection entre les deux ?
