bonjour
voila j'ai un ensemble Z[i] = {z/ z appartient à C , il existe (a,b) appartient à Z², z = a+ ib}
et je dois déterminer les elements inversibles de Z[i]
ma correction d'exercice est : un element z = a + ib de C* est inversible et son inverse est 1/z = a -ib/a+ib
(déja je ne conprend pas pourquoi 1/z est égal à ca mais pas à 1 / a + ib)
un element z = a+ib de Z[i] \ {0} est inversible ssi a- ib / a+ ib est dans Z[i]
Si a/ a² + b² et -b/a²+b² sont dans Z alors a²/ (a²+b²) et b²/(a²+b²)² son dans N ( pourquoi on prend a/a²+b² et -b/a²+b² ? comment à t'on l'idée de prendre ca ? )
d'ou a²/(a²+b²)² + b²/(a²+b²)² = a²+b² / (a²+b²)² = 1/ a²+b² ( en fait je ne vois pas ou veut on en venir ? avec tout ca ?)
(a,b) = (1,0) ou (-1,0) ou ( 0,1) ou ( 0,-1 ) ( pourquoi ?)
réciproquement pour ces valeurs de a et b a-ib / a²+b² est dans Z [i]. les inversibles sont donc 1,-1 , i et -i
merci de m'expliquer car je n'ai vraiment pas compris la correction ni le fil conducteur du truc
Besoin d'explication sur les anneaux
7 messages
- Page 1 sur 1
lanapurna16 a écrit:bonjour
voila j'ai un ensemble Z[i] = {z/ z appartient à C , il existe (a,b) appartient à Z², z = a+ ib}
et je dois déterminer les elements inversibles de Z[i]
ma correction d'exercice est : un element z = a + ib de C* est inversible et son inverse est 1/z = a -ib/a+ib
Tu calcules
Réciproquement, si z est inversible et z' est son inverse, alors
Bonjour,
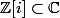
Supposons que z soit inversible, alors pour tout z dans C* (i.e (a,b) (0,0)), on a:
(0,0)), on a:
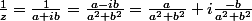 . Donc
. Donc 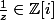 , avec
, avec 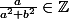 et
et 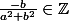 .
.
Donc^2} \in \mathbb{N}) ,
, ^2} \in \mathbb{N}) et la somme de ces deux termes donne
et la somme de ces deux termes donne 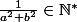 . Donc, pour que z soit inversible, il faut que
. Donc, pour que z soit inversible, il faut que 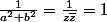 , c'est-à-dire que qu'on ait les couples solutions (a,b) suivants :
, c'est-à-dire que qu'on ait les couples solutions (a,b) suivants :  \ ; \ (0,\pm 1)) ce qui donne les inverses suivants :
ce qui donne les inverses suivants : 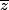 = -1 ou 1 ou i ou -i
= -1 ou 1 ou i ou -i
Bon, on retrouve ces solutions rapidement avec ce qu'a écrit ev85, mais j'essayais de rédiger en fonction de ce que tu avais écrit.
Supposons que z soit inversible, alors pour tout z dans C* (i.e (a,b)
Donc
Bon, on retrouve ces solutions rapidement avec ce qu'a écrit ev85, mais j'essayais de rédiger en fonction de ce que tu avais écrit.
lanapurna16 a écrit:bonjour
voila j'ai un ensemble Z[i] = {z/ z appartient à C , il existe (a,b) appartient à Z², z = a+ ib}
et je dois déterminer les elements inversibles de Z[i]
ma correction d'exercice est : un element z = a + ib de C* est inversible et son inverse est 1/z = a -ib/a+ib
(déja je ne conprend pas pourquoi 1/z est égal à ca mais pas à 1 / a + ib)
un element z = a+ib de Z[i] \ {0} est inversible ssi a- ib / a+ ib est dans Z[i]
Si a/ a² + b² et -b/a²+b² sont dans Z alors a²/ (a²+b²) et b²/(a²+b²)² son dans N ( pourquoi on prend a/a²+b² et -b/a²+b² ? comment à t'on l'idée de prendre ca ? )
d'ou a²/(a²+b²)² + b²/(a²+b²)² = a²+b² / (a²+b²)² = 1/ a²+b² ( en fait je ne vois pas ou veut on en venir ? avec tout ca ?)
(a,b) = (1,0) ou (-1,0) ou ( 0,1) ou ( 0,-1 ) ( pourquoi ?)
réciproquement pour ces valeurs de a et b a-ib / a²+b² est dans Z [i]. les inversibles sont donc 1,-1 , i et -i
merci de m'expliquer car je n'ai vraiment pas compris la correction ni le fil conducteur du truc
l'anneau s'appelle l'anneau de Gauss: en fait un element a est inversible s'il existe un element b tel
que a*b =1 tu ecris b =x+iy et tu trouves la solution du prof
mais j'ai une autre question ou je n'ai pas compris
soit I l'idéal de Z [i] engendré par z. on note F le quotient de Z[i] par I
quel est le cardinal de F?
la mon prof a fait intervenir les classe d'équivalences je ne sais pas pourquoi ? quel est le lien avec le cardinal ?
en fait il a écrit : notons ^z la classe d'équivalence d'un elt z de Z[i] module I; Deux elements z= a+ib et z'= a'-ib' représente le meme elt de F ssi z-z' est dans I
or z-z' I <=> (a-a') + i(b-b') I
<=> il existe c et d Z², (a-a') +i(b-b') = z(c+id)
<=> a-a' zZ et b-b' zZ.
les elts de F sont donc ^1 ^2 ^0 ^i ^1+i ^1+2i ^2+i 2+2i
et j'ai marqué que le cardinal de F est donc g mais j'ai surement voulu écrire 9
je n'ai pas saisi la corection ni le fil conducteur en faite il veut en venir ou ?
soit I l'idéal de Z [i] engendré par z. on note F le quotient de Z[i] par I
quel est le cardinal de F?
la mon prof a fait intervenir les classe d'équivalences je ne sais pas pourquoi ? quel est le lien avec le cardinal ?
en fait il a écrit : notons ^z la classe d'équivalence d'un elt z de Z[i] module I; Deux elements z= a+ib et z'= a'-ib' représente le meme elt de F ssi z-z' est dans I
or z-z' I <=> (a-a') + i(b-b') I
<=> il existe c et d Z², (a-a') +i(b-b') = z(c+id)
<=> a-a' zZ et b-b' zZ.
les elts de F sont donc ^1 ^2 ^0 ^i ^1+i ^1+2i ^2+i 2+2i
et j'ai marqué que le cardinal de F est donc g mais j'ai surement voulu écrire 9
je n'ai pas saisi la corection ni le fil conducteur en faite il veut en venir ou ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
