Salut,
Je comprend pas trop ce que tu bricole.
Si je comprend bien, ton espace vectoriel, c'est
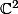
vu comme

- espace vectoriel (donc de dimension 4) et ta base, c'est
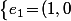\,;\,e_2\!=\!(i,0)\,;\,e_3\!=\!(0,1)\,;\,e_4\!=\!(0,i)\big\})
.
Si c'est effectivement ça, la base duale, c'est complètement couillon, c'est
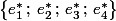
avec, pour tout
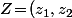\!\in\!\mathbb C^2\ \ ,\ \ e_1^*(Z)\!=\!\text{R\'e}(z_1)\ ;\ e_2^*(Z)\!=\!\text{Im}(z_1)\ ;\ e_3^*(Z)\!=\!\text{R\'e}(z_2)\ ;\ e_4^*(Z)\!=\!\text{Im}(z_2)\ ;\)
Ou alors, c'est que tu parle de base duale au sens des espaces euclidiens où il y a un isomorphisme naturel entre l'espace vectoriel et son dual et où, en conséquence, on peut voir la base duale comme formée de vecteurs et pas de forme linéaires.
Sauf que, dans ce cas là, ben peut-être qu'il faudrait penser à préciser quel est le produit scalaire que tu considère sur ton espace, non ?
Par exemple, si tu prend le premier produit scalaire qui vient à l'esprit, à savoir
\,|\,(a'\!+\!ib',c'\!+\!id')\big>=aa'\!+\!bb'\!+\!cc'\!+\!dd')
pour tout
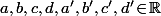
alors ta base est orthonormée donc la base duale, ben c'est elle même.
Mais bien sûr, ça pourrait être autre chose avec un produit scalaire différent...
P.S. En fait, en réfléchissant un peu, je me demande si ce que tu as considéré, c'est pas une forme hermitienne
sur un espace vectoriel réel, ce qui n'a pas le moindre sens : comment diable veut-tu avoir une application

- linéaire sur un e.v. réel ????
(une forme hermitienne, ça doit en particulier être

- linéaire par rapport à la première variable)
