Arithmétique pour l'honneur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
foxto
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Sep 2006, 19:42
-
 par foxto » 14 Déc 2006, 20:14
par foxto » 14 Déc 2006, 20:14
Excusez moi de vous resoliciter pour le probleme d'arithmétique suivant :
p étant premier (supérieur a 5) , montrer que

est la somme de 3 carrés ...
Depuis 2 jours ke l'on m'a posé le probleme, les moqueries fusent... AIdez moi, pour que je garde encire quelque dignité !
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 05:56
par Zebulon » 21 Déc 2006, 05:56
Bonjour,
foxto a écrit:Excusez moi de vous resoliciter pour le probleme d'arithmétique suivant :
p étant premier (supérieur a 5) , montrer que

est la somme de 3 carrés ...
Depuis 2 jours ke l'on m'a posé le probleme, les moqueries fusent... AIdez moi, pour que je garde encire quelque dignité !
on a le droit à la solution triviale :
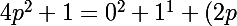^2)
? :we:
-
c pi
- Membre Rationnel
- Messages: 596
- Enregistré le: 09 Sep 2006, 18:03
-
 par c pi » 21 Déc 2006, 11:24
par c pi » 21 Déc 2006, 11:24
Bonjour
foxto a écrit:Depuis 2 jours ke l'on m'a posé le probleme, les moqueries fusent... AIdez moi, pour que je garde encire quelque dignité !
Laisse-les se gausser
et passe dignement ton chemin, par
là ! :zen:
Pour que
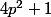
ne soit pas la somme de trois carrés,
il faudrait donc qu'il soit de la forme
)
avec

et

entiers positifs.
Or dans les conditions données
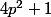
est impair
alors que
)
est pair.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 21 Déc 2006, 12:05
par fahr451 » 21 Déc 2006, 12:05
je n'ai jamais vu de preuve du théorème de lagrange sur les sommes de trois carrés;quelqu'un aurait -il un lien ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Déc 2006, 12:31
par yos » 21 Déc 2006, 12:31
c pi a écrit:il faudrait donc qu'il soit de la forme
)
avec

et

entiers positifs.
Or dans les conditions données
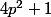
est impair
alors que
)
est pair.
h=0 est autorisé. Mais ici c'est pas le problème.
-
c pi
- Membre Rationnel
- Messages: 596
- Enregistré le: 09 Sep 2006, 18:03
-
 par c pi » 21 Déc 2006, 14:24
par c pi » 21 Déc 2006, 14:24
yos a écrit:h=0 est autorisé.
Cela m'avait échappé, merci ! :++:
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 21 Déc 2006, 21:40
par BQss » 21 Déc 2006, 21:40
c pi a écrit:Bonjour
Laisse-les se gausser
et passe dignement ton chemin, par
là ! :zen:
Pour que
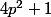
ne soit pas la somme de trois carrés,
il faudrait donc qu'il soit de la forme
)
avec

et

entiers positifs.
Or dans les conditions données
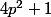
est impair
alors que
)
est pair.
Il faudrait donc que tu t'assures egalement qu'il n'a pas un reste de 7 dans la division par 8 si je ne m'abuse, dans le cas ou h=0, ce sont les seuls nombres impaires a exclure(15 n'est pas la somme de 3 carrés par exemple).
Mais comme 4p^2+1 a soit un reste de 1 quand p^2 est impaire soit un reste de 5 quand p^2 est paire dans la division par 8 , il n'y a pas grand chose a rajouter et c'est prouvé...
Sinon la reponse de zebulon marche tres bien de toute facon.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Déc 2006, 21:46
par yos » 21 Déc 2006, 21:46
Foxto avait déjà posé le problème et semblait vouloir une solution non triviale comme :

,

,

,

,
...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 101 invités
est la somme de 3 carrés ...
ne soit pas la somme de trois carrés,
)
et
entiers positifs.
est impair
est pair.