Arithmétique dans Z
64 messages
- Page 3 sur 4 - 1, 2, 3, 4
mais si
la question suivante est plus dure
en partant de a premier avec m et b premier avec n il faut prouver que r est premier avec mn et comme m et n sont premiers entre eux il suffit de prouver que r est premier avec m et avec n
avec m ?
an+bm = mnq + r
soit d un diviseur commun à m et r alors d divise an mais comme comme d est premier avec n on a d divise a et d est commun à m et a donc d = 1
idem avec n .
donc la restriction f * de f est bien définie elle reste injective comme restriction d une injection
reste à prouver que f* est surjective
soit r ds tmn comme f est surjective il existe a et b tels que f(a,b) = r
reste à prouver que nécessairement a est premier avec m et b avec n
(un peu comme je l'ai fait avant)
la question suivante est plus dure
en partant de a premier avec m et b premier avec n il faut prouver que r est premier avec mn et comme m et n sont premiers entre eux il suffit de prouver que r est premier avec m et avec n
avec m ?
an+bm = mnq + r
soit d un diviseur commun à m et r alors d divise an mais comme comme d est premier avec n on a d divise a et d est commun à m et a donc d = 1
idem avec n .
donc la restriction f * de f est bien définie elle reste injective comme restriction d une injection
reste à prouver que f* est surjective
soit r ds tmn comme f est surjective il existe a et b tels que f(a,b) = r
reste à prouver que nécessairement a est premier avec m et b avec n
(un peu comme je l'ai fait avant)
Je vais essayer de traduire pour vérifier jusqu'où je comprends :
On a :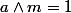 et
et 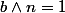
Est-ce que ceci vient bien du fait qu'on puisse parler du reste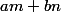 (déjà là je suis pas sûr du pourquoi !)
(déjà là je suis pas sûr du pourquoi !)
Ensuite, il faut montrer que :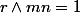 à partir de ce qui précède (Là non plus je ne comprends pas pourquoi il faut faire ceci !)
à partir de ce qui précède (Là non plus je ne comprends pas pourquoi il faut faire ceci !)
ceci vient bien du fait que : si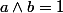 et
et 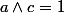 alors
alors 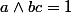
(dans le Cours on aavait juse vu l'mplication : je savais pas qu'il y avait la réciproque)??
On a :
Est-ce que ceci vient bien du fait qu'on puisse parler du reste
Ensuite, il faut montrer que :
il faut prouver queest premier avec
et comme
et
sont premiers entre eux il suffit de prouver que
est premier avec
et avec
:
ceci vient bien du fait que : si
(dans le Cours on aavait juse vu l'mplication : je savais pas qu'il y avait la réciproque)??
aie pour moi sur un point
si r est premier avec m et n, r est premier avec mn INUTILE que m et n soient premiers entre eux ici .
sinon
le reste de la division existe tjrs que a et b soient premiers avec m et n ou non peu importe
mais on veut que r soit dans tmn lorsque a est dans tm et b dans tn
pour pouvoir considérer la restriction
si r est premier avec m et n, r est premier avec mn INUTILE que m et n soient premiers entre eux ici .
sinon
le reste de la division existe tjrs que a et b soient premiers avec m et n ou non peu importe
mais on veut que r soit dans tmn lorsque a est dans tm et b dans tn
pour pouvoir considérer la restriction
Bonsoir,
A partir de là je ne comprends pas très bien :
A partir de là je ne comprends pas très bien :
fahr451 a écrit:
an+bm = mnq + r
soit d un diviseur commun à m et r alors d divise an mais comme comme d est premier avec n on a d divise a et d est commun à m et a donc d = 1
idem avec n .
donc la restriction f * de f est bien définie elle reste injective comme restriction d une injection
reste à prouver que f* est surjective
soit r ds tmn comme f est surjective il existe a et b tels que f(a,b) = r
reste à prouver que nécessairement a est premier avec m et b avec n
(un peu comme je l'ai fait avant)
64 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
