Arithmétique dans Z
64 messages
- Page 2 sur 4 - 1, 2, 3, 4
pouik a écrit:oui mais dans notre situation, que vaut(i.e. la puissance à laquelle il faut s'arrêter) ?
il autre termes (
pouik a écrit:PS : pour aviateurpilot,
J'ai un exo sur la fonction indicatrice d4euler (c'est de l'arithmétique comme vous aimez) que je n'arrive pas à résoudre entièrement.
Donc si vous êtes preneur, ça m'arrangerais énormément. :zen:
quel est ce exo?
okay je comprends, merci.
donc le problème est le suivant :
Notations : pour tout entier supérieur ou égal à
supérieur ou égal à  :
:
-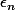 désigne l'ensemble des entiers
désigne l'ensemble des entiers 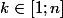 tels que
tels que 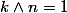 .
.
-) désigne le cardinal de
désigne le cardinal de 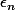 , c'est-à-dire
, c'est-à-dire ) est le nombre d'entiers compris au sens large entre
est le nombre d'entiers compris au sens large entre  et
et  qui sont premiers avec
qui sont premiers avec  .
.
1. Quelques valeurs de ... Soit
... Soit 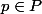 .
.
(a) Déterminer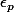 et en déduire
et en déduire ) .
.
(b) Mêmes questions avec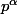 , où
, où 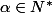 . On déterminera d'abord les entiers de
. On déterminera d'abord les entiers de 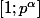 qui ne sont pas premiers avec
qui ne sont pas premiers avec 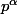 .
.
2. Carcatère multiplicatif de . Soient
. Soient 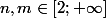 tels que
tels que 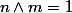 .
.
On considère l'application qui à tout couple
qui à tout couple  \in [ 0;m-1] \times [ 0;n-1 ]) associe le reste de la division euclidienne de
associe le reste de la division euclidienne de 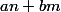 par
par 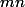 , situé, dans
, situé, dans 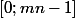 .
.
(a) Montrer que est injective.
est injective.
(b) Montrer que est bijective.
est bijective.
(c) Montrer que induit une bijection de
induit une bijection de 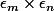 sur
sur 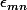 , et conclure.
, et conclure.
3. Une expression de) pour
pour  quelconque... Soit
quelconque... Soit 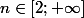 et
et 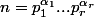 sa décomposition en facteurs premiers. Etablir :
sa décomposition en facteurs premiers. Etablir :
 = n\left(1 - \frac{1}{p_1}\right) ... \left(1 - \frac{1}{p_r}\right))
Donc moi j'ai réussi à faire le 1. seulement (et en plus je n'arrive pas bien à justifier mes réponses). Merci d'avance pour votre aide. :we:
donc le problème est le suivant :
Notations : pour tout entier
-
-
1. Quelques valeurs de
(a) Déterminer
(b) Mêmes questions avec
2. Carcatère multiplicatif de
On considère l'application
(a) Montrer que
(b) Montrer que
(c) Montrer que
3. Une expression de
Donc moi j'ai réussi à faire le 1. seulement (et en plus je n'arrive pas bien à justifier mes réponses). Merci d'avance pour votre aide. :we:
64 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
