Salut,
mehdi-128 a écrit:{0x} {1x} {2x} ... {jx} ... {Nx} où

Je comprends pas comment on sait que chacun de ces réels sera dans
l'intervalle

etc ...
Le problème, c'est d'avant même apprendre les maths., ça serait utile d'apprendre à lire (et à comprendre ce qu'on lit) : ce que ton papier dit, ce n'est 'est
sûrement pas que chacun des réels est dans
LE (article défini) intervalle

etc .. mais que chacun de ces réels est dans
UN DES (article indéfini) intervalles

...
Ce qui est évidement une évidence évidente (!!!) vu que par définition (de {.}) les réels en questions sont dans [0,1[ et que les intervalles

etc .. forment une partition de [0,1[.
Et bien sûr, ce "UN DES" (et pas LE) ne dit absolument rien concernant la répartition des réels en question dans les différents intervalles : il n'est à priori pas exclu qu'ils soient tous dans le même intervalle. Par contre, la déduction concon qu'on peut faire, c'est que, vu que le nombre (N) d'intervalle est strictement plus petit que le nombre (N+1) de réels, ben y'a forcément au moins un des intervalles qui contient strictement plus d'un des réels :
Il existe
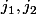 distincts
distincts et

tels que

et

soient dans le même

.
Donc

et vu que

et

avec

, cela signifie que
x\!-\!(p_1\!-\!p_2)\big|\!<\!\frac{1}{N})
c'est à dire que

avec

et
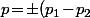\!\in\!{\mathbb Z})
.
