Applications linéaires
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Marion1
- Messages: 2
- Enregistré le: 25 Mar 2010, 16:09
-
 par Marion1 » 25 Mar 2010, 16:12
par Marion1 » 25 Mar 2010, 16:12
Bonjour, j'ai un petit souci sur un exercice, je me permet de vous demander de l'aide... Voici l'énoncé :
E Kev de dimension finie, f endormophisme tel que

et
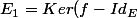)
,
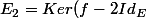)
, je dois montrer que E1 et en somme directe avec E2 et déterminer l'expression sur projecteur p1 (sur E1 parallèlement à E2) et p2 (sur E2 parallèlement à E1) en fonction de f.
Je ne vois absolument pas comment faire, j'ai essayé de montrer la somme directe de plusieurs façons mais aucune n'aboutit !
Merci pour vos conseils

-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 25 Mar 2010, 17:00
par Joker62 » 25 Mar 2010, 17:00
Bonjour.
Quel niveau tu as ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Mar 2010, 17:01
par Nightmare » 25 Mar 2010, 17:01
Salut !
1) Tu peux remarquer que

équivaut à
(f-2Id)=0)
, d'où le fait qu'on introduise E1 et E2.
2) Ensuite, ce qui est important aussi (pour une généralisation), c'est que les polynômes X-1 et X-2 sont premiers entre eux, en particulier, on a
+(X-2)=1)
.
Du coup, si l'on se fixe x dans E, on peut écrire que
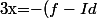+(f-2Id)\)(x)=-(f-Id)(x)+(f-2Id)x)
qui est bien dans

. Reste à montrer que la somme est directe, c'est à dire que E1 et E2 sont disjoints. Je te laisse essayer.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 25 Mar 2010, 17:04
par skilveg » 25 Mar 2010, 17:04
Disjoints, Nightmare? ;)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 25 Mar 2010, 17:08
par Joker62 » 25 Mar 2010, 17:08
On peut pas lui reprocher avec le beau ptit post qu'il nous a mis.
On va dire qu'il était distrait lol
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Mar 2010, 17:13
par Nightmare » 25 Mar 2010, 17:13
Disjoint au 0 près :D
-
Marion1
- Messages: 2
- Enregistré le: 25 Mar 2010, 16:09
-
 par Marion1 » 25 Mar 2010, 17:51
par Marion1 » 25 Mar 2010, 17:51
Bonjour à vous,
Je suis en sup ;)
Nightmare, c'est vraiment clair, merci beaucoup. J'avais essayé de faire apparaître cette forme de x, mais bon, sans succès !
Donc pour montrer que l'intersection est nul, c'est pas dur :
Soit X de E1, alors f(X)=X, soit X de E2, alors f(X)=2X d'où 2X=X, ie X=0... :)
Par contre pour les projecteurs, je ne vois pas trop, pouvez vous me donner une petite indication ?
;)
 par alavacommejetepousse » 26 Mar 2010, 07:58
par alavacommejetepousse » 26 Mar 2010, 07:58
bonjour
tite remarque de rédaction
si tu dis "soit X dans E1 et soit X dans E2 " alors a priori ce ne sont pas les mêmes X et donc il faudrait prendre X et X'
toi tu prends un X ds E1 et E2 donc " soit X dans E1 et E2" ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités