Application bilinéaire

[Marie44]

Bonjour, j'aimerai savoir comment montrer qu'une application bilinéaire B(x,y) est continue. Merci d'avance

[Galt]

Bonjour
Comme , il suffit de montrer qu'elle est continue en (0,0)
Sur un espace vectoriel de dimension finie, c'est évident, car toutes les applications linéaires sont continues.
En dimension infinie, je ne sius pas certain que toutes les applications bilinéaires soient continues, même si je n'ai pas de contre-exemple en tête
Est-ce qu'on connait B, ou bient doit-on montrer que toutes les applications bilinéaires sont continues ?

[Marie44]

Bonjour, merci por la reponse, en fait il faut montrer que
B est continue ssi il existe une constante M tq:
pour tout (x,y) ||B(x,y)||< ou = M.||x||.||y||
Meme en utilisant la continuité en zero, je ne vois pas comment montrer la double implication.

[Galt]

On progresse, on est dans un espace vectoriel normé.
Si la constante M existe, alors c'est clair que B est continue.
Je pense que la réciproque se fait un peu de la même manière que pour montrer que les applications linéaires continues vérifient , en considérant l'image réciproque de la boule unité, qui contient une boule de rayon R (puisque pour tout 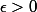il existe 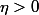tel que entraîne on prend 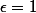, et on a .
Avec une application bilinéaire, on doit pouvoir s'en sortir d'une manière analogue.