Analyse Complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 17 Juin 2017, 06:40
par checkmaths » 17 Juin 2017, 06:40
Bonjour, je suis aussi entrain de refaire mon examen d'Analyse Complexe de juin 2017 et je l'ai déjà bien entamé

Mais fallait bien évidemment que je tombe sur un exercice où tu restes perplexe...

Voici l'exercice :
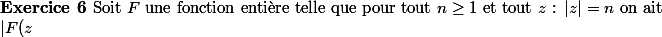|\leq\frac{1}{n}\textrm{. Montrer que }F\textrm{ est identiquement nulle.})
Pourriez-vous m'aider svp ?



-
aviateur
 par aviateur » 17 Juin 2017, 08:32
par aviateur » 17 Juin 2017, 08:32
Bonjour Penses au principe du maximum.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 17 Juin 2017, 12:53
par pascal16 » 17 Juin 2017, 12:53
Je ne suis pas spécialiste, mais parle-t-on bien de fonctions entières ie, les déformations du plan ?
soit f(z)=z/|z|² pour |z| >1 raccordée à une boule pour avoir la dérivabilité et la continuité en |z|=1, elle doit convenir.
ou du ça en révolution :

c'est bien une déformation continue du plan , donc une fonction entière

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 17 Juin 2017, 13:30
par capitaine nuggets » 17 Juin 2017, 13:30
Salut !
A mon avis, ce qu'on entend ici par fonction entière, c'est fonction d'une variable complexe holomorphe sur

tout entier.


-
Lostounet
- Modérateur
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 17 Juin 2017, 17:46
par Lostounet » 17 Juin 2017, 17:46
capitaine nuggets a écrit:Salut !
A mon avis, ce qu'on entend ici par fonction entière, c'est fonction d'une variable complexe holomorphe sur

tout entier.

C'est marrant... ! puisque "holomorphe" provient étymologiquement de "holo" = entier et "morphe" = forme. Et que les fonctions holomorphes sur C (entières) sont des transformations conformes qui préservent localement les angles.
Ce à quoi pense Pascal n'est pas si loin de la définition???

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 17 Juin 2017, 19:27
par checkmaths » 17 Juin 2017, 19:27
J'ai trouvé ceci sur exo7 :
\neq0\textrm{ et notons }\alpha=|F(z)|>0\textrm{. Si }n>1\textrm{ tel que }\frac{1}{n}<\alpha\textrm{, alors}\\\textrm{le principe du maximum affirme que }|F(z)|<\frac{1}{n}<\alpha\textrm{ pour tout }|z|<n\textrm{. Contradiction.})
Mais je ne vois pas pq le

affirme ce qu'il y a au dessus...
Pourriez-vous m'expliquer svp ?



-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 17 Juin 2017, 20:11
par pascal16 » 17 Juin 2017, 20:11
Y a un Théorème de Liouville.
Les démos dépassent mes compétences.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 17 Juin 2017, 20:23
par jlb » 17 Juin 2017, 20:23
Que dit ce théorème, sur le maximum de |f| sur l'adhérence de U si f n'est pas constante?
Mais je maintiens : en utilisant la formule de Cauchy et une petite majoration le résultat tombe tout aussi simplement!! Surtout quand on ne connaît pas le th utilisé...
Et pour reprendre ce que tu proposes: tu considères que ta fonction est non constante ( sinon c'est facile)
Ensuite tu considères zo dans C pour montrer que F(zo) = 0
Si c'est le cas, il n'y a rien à faire. Sinon, tu choisis n entier tel que |zo|<n et tu utilises le principe du maximum sur le disque de centre O et de rayon n alors le maximum de |f| est atteint en z1 de module n et
|F(zo)|=<|F(z1)|=< 1/n. Ceci valant pour tout n supérieur au module de zo, tu en déduis que F(zo) =0
( c'est l'idée de la démo par l'absurde proposée: tu choisis n tel que 1/n <alpha et |n|> |zo| ( zo initial tel que |F(zo)|=alpha) alors alpha= |F(zo)| =< Max|F(z)|_{pour z sur le bord du disque de rayon n}=< 1/n < alpha d'où l'absurdité: alpha <alpha
Avec le th de Cauchy: pour zo dans C et n>|zo|, comme F est holomorphe,
F(zo) = (1/(2ipi)) intégrale_sur_le_bord_du disque_de_rayon_ n F(z)/(z-zo) dz
d'où |F(zo)|=< 1/(2(npi(n-|zo|))) x intégrale_de_0_à_2pi n dthéta = 1/(n-|zo|)
ce qui donne le résultat
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 17 Juin 2017, 21:07
par checkmaths » 17 Juin 2017, 21:07
Merci à tous j'ai compris et, du coup, terminé de refaire l'examen


Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités










tout entier.



