6122 résultats trouvés
Revenir à la recherche avancée
jorgeantoine a écrit:mais donc
S4= 1/(1x2) + 1/(2x3) + 1/(3x4) + 1/(4x5)
Eh oui !
- par Sa Majesté
- 04 Déc 2021, 20:21
-
- Forum: ✎✎ Lycée
- Sujet: suite
- Réponses: 23
- Vues: 908
Non
S3=1/(1x2) + 1/(2x3) + 1/(3x4)
- par Sa Majesté
- 04 Déc 2021, 19:19
-
- Forum: ✎✎ Lycée
- Sujet: suite
- Réponses: 23
- Vues: 908
Sn=1/(1x2) + 1/(2x3) + 1/(3x4) + ....... + 1/(n(n+1))
S1=1/(1x2)
S2=1/(1x2) + 1/(2x3)
etc
- par Sa Majesté
- 04 Déc 2021, 19:03
-
- Forum: ✎✎ Lycée
- Sujet: suite
- Réponses: 23
- Vues: 908
jorgeantoine a écrit:Je pense que la realtion de récurrence est Sn= Sn-1 +1/n(n+1)
Oui
jorgeantoine a écrit:et pour S1= 1/2
S2=1/6
S3=1/12
S4=1/20
Non, là tu as calculé 1/(n(n+1))
- par Sa Majesté
- 04 Déc 2021, 18:46
-
- Forum: ✎✎ Lycée
- Sujet: suite
- Réponses: 23
- Vues: 908
Ecris Sn, écris S(n-1) et fais la différence.
Pour t'aider tu peux commencer en fixant une valeur de n (n=3 par ex).
- par Sa Majesté
- 04 Déc 2021, 18:23
-
- Forum: ✎✎ Lycée
- Sujet: suite
- Réponses: 23
- Vues: 908
Soit P le périmètre de la fenêtre.
Que vaut P en fonction de h et r.
En déduire h en fonction de r (et de P supposé fixe).
Qua vaut A en fonction de h et r.
Remplacer h par son expression en fonction de r et P.
Calculer la valeur de r (fonction de P) qui maximise A.
- par Sa Majesté
- 28 Nov 2021, 20:08
-
- Forum: ✎✎ Lycée
- Sujet: Question d’optimisation
- Réponses: 6
- Vues: 374
Yoyo1293 a écrit:Du coup j'ai pensé à une autre méthode de faire un changement de variable cos(x)=X ça semble fonctioné mais je ne sais pas si c'est une bonne méthode.
C'est une bonne méthode.
- par Sa Majesté
- 27 Nov 2021, 14:11
-
- Forum: ✯✎ Supérieur
- Sujet: fonction trigonométrique
- Réponses: 10
- Vues: 368
83 R² = 6.043037 (1 - R²)
83 R² = 6.043037 - 6.043037 R²
83 R² + 6.043037 R² = 6.043037
(83 + 6.043037) R² = 6.043037
89.043037 R² = 6.043037
R² = 6.043037 / 89.043037
- par Sa Majesté
- 24 Nov 2021, 21:12
-
- Forum: ✯✎ Supérieur
- Sujet: Isoler un terme
- Réponses: 2
- Vues: 296
Odry a écrit:Ah oui merci
-1/n+ (1/(n+3)^3) >= -1/(n+1)
Ce ne serait pas plutôt -1/n+ (1/(n+
1)^3)
< = -1/(n+1) ?
- par Sa Majesté
- 21 Nov 2021, 21:32
-
- Forum: ✎✎ Lycée
- Sujet: La constance d’apéry
- Réponses: 26
- Vues: 713
HiedakiTora22 a écrit:Pour la démonstration de l'équivalence j'ai réussi mais pour la question 2 je ne suis pas sûr de bien comprendre ce que vous voulez faire, je ne dirais pas non a d'autres explications
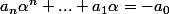

divise à gauche donc à droite
- par Sa Majesté
- 21 Nov 2021, 18:07
-
- Forum: ✎✎ Lycée
- Sujet: Maths Expertes Dm (Chapitre Congruences)
- Réponses: 4
- Vues: 578
Bonjour, digischool doit protéger rapidement le site maths-forum du spam et des hackers, sinon, on risque d'avoir des centaines de posts frauduleux qui empecheront de trouver les posts de maths dans cet océan de spams On a déjà des centaines de posts frauduleux. Fort heureusement, ceux-ci arrivent ...
- par Sa Majesté
- 21 Nov 2021, 18:00
-
- Forum: ⚑ À propos de ce site
- Sujet: se protéger du spam
- Réponses: 16
- Vues: 2370
(b) Montrer que f-¹(AUB) = f-¹(A) U f-¹(B). Il faut montrer une égalité entre 2 ensembles. En général, ça se fait en démontrant la double inclusion. 1ère partie : f-¹(AUB) inclus dans f-¹(A) U f-¹(B) L'inclusion se montre en général en prenant un élément quelconque du premier ensemble et en démontr...
- par Sa Majesté
- 13 Nov 2021, 20:23
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstrations algébriques
- Réponses: 2
- Vues: 274