88 résultats trouvés
Revenir à la recherche avancée
Exercice sur les suites
Bonjour, Pourriez-vous m'aider s'il vous plaît pour cette exercice concernant le chapitre des suites. Voici les questions : 1) Soit (v_{n} ) la suite définie par (u_{n} ) : \left \{ {{u_{0} =5} \atop {Pour tout n\geq0,u_{n+1}=-5+u_{n} }} \right. (v_{n} ): v_{n} =\sum_{k=0}^n ...
- 30 Sep 2018, 13:19
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 12
- Vues: 303
- 29 Sep 2018, 20:56
- Forum: ✎✎ Lycée
- Sujet: Exercice concernant les suites
- Réponses: 18
- Vues: 580
Re: Exercice concernant les suites
Donc,
1) a)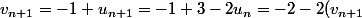=2-2v_{n} -2=-2v_{n})
1) a)
- 29 Sep 2018, 20:42
- Forum: ✎✎ Lycée
- Sujet: Exercice concernant les suites
- Réponses: 18
- Vues: 580
Exercice concernant les suites
Bonsoir, Pourriez-vous me corriger s'il vous plaît pour cette exercice concernant le chapitre des suites. Soit (u_{n} ) la suite définie par : (u_{n} )\left \{ {{u_{0} =2} \atop {u_{n+1}=3-2u_{n} }} \right. Calculer 1)a) u_{1} u_{2} u_{3} u_{4} 2)On définit (v_{n} ) la suite ...
- 29 Sep 2018, 20:16
- Forum: ✎✎ Lycée
- Sujet: Exercice concernant les suites
- Réponses: 18
- Vues: 580
Re: Exercice sur les suites
Merci pour votre aide et bonne soirée.
- 29 Sep 2018, 19:34
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 10
- Vues: 442
Re: Exercice sur les suites
hdci a écrit:C'est exact ! (mais le calcul de, s'il est utile pour avoir
, n'est pas demandé dans l'énoncé ; il ne doit figurer que comme justification dans la question b)
D'accord
- 29 Sep 2018, 19:32
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 10
- Vues: 442
Re: Exercice sur les suites
Je vous explique tout, comme j'ai plein d'autres exercices à faire j'ai rédiger celui là sur le forum, en cherchant rapidement de mon coté.
Je vous assure, j'en ai bien fait des plus compliqué en classe.
Je vous assure, j'en ai bien fait des plus compliqué en classe.
- 29 Sep 2018, 19:31
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 10
- Vues: 442
Re: Exercice sur les suites
On a donc : (1-\frac{25}{100} )=\frac{3}{4}=0,75 De plus u_{0}=120 et u_{n+1}=0,75u_{n}+14 a) Première semaine : u_{1}=0,75u_{0}+14=u_{1}=0,75*120+14=104 Deuxième semaine : u_{2}=0,75u_{1}+14=0,75*104+14=92 b) Troisième semaine : u_{3}=0,75u_{2}+14=0,75*92+14=83 c) u_{n+1}=0,75u_{n}+14
- 29 Sep 2018, 19:25
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 10
- Vues: 442
Exercice sur les suites
Bonsoir, Pourriez-vous m'aider s'il vous plaît pour cette exercice concernant le chapitre des suites. 7) a) Mohamed suit 120 comptes sur un réseau social et ne parvient plus à suivre tous les statuts de ces connaissances. Il décide donc, chaque semaine, de retirer 25% des comptes qu'il suit et de n'...
- 29 Sep 2018, 18:24
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les suites
- Réponses: 10
- Vues: 442
Re: Exercice, sur les produits scalaires.
Désolé, j'ai voulu rédiger trop rapidement. Nous avons alors. ||-6u – 2v|| = (-6u – 2v).(-6u – 2v) Calculons donc (-6u – 2v).(-6u – 2v). (-6u – 2v).(-6u – 2v) = -6u.(-6u) + (-6u).(-2v) + (-2v).(-6u) + (-2v).(-2v) = 36u.u + 12u.v + 12v.u + 4v.v = 36u.u + 24u.v + 4v.v =36u² + 24u.v + 4v² Ainsi, u est ...
- 26 Mai 2018, 15:10
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Merci, normalement je ne me suis pas trompé dans les calcules. Donc du coup pour la question 2). On a ||-6u – 2v|| = (-6u – 2v).(-6u – 2v) Calculons donc (-6u – 2v).(-6u – 2v). (-6u – 2v).(-6u – 2v) = -6u.(-6u) + (-6u).(-2v) + (-2v).(-6u) + (-2v).(-2v) = 36u.u + 12u.v + 12v.u + 4v.v = 4u.u + 12u.v +...
- 25 Mai 2018, 21:03
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
- 25 Mai 2018, 20:52
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Oui, bien sûr
Donc pour la question 2)
Il faut juste dire ||2u+3v||=√120
Donc pour la question 2)
Il faut juste dire ||2u+3v||=√120
- 25 Mai 2018, 20:47
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Prenons l'exemple de 25, effectivement √25 = 5 alors que 25^2 = 625, je n'ai pas bien rédiger le résonnement
Mon idée était d'écrire √25 = 5 donc 5^2=25.
Mon idée était d'écrire √25 = 5 donc 5^2=25.
- 25 Mai 2018, 20:35
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Oui bien sur je connais la notion de "racine carrée" .
On a ainsi, √x = x²
J'ai juste voulu précisé, donc pour en déduire ||2u+3v||.
Il faut juste dire ||2u+3v||=√120.
On a ainsi, √x = x²
J'ai juste voulu précisé, donc pour en déduire ||2u+3v||.
Il faut juste dire ||2u+3v||=√120.
- 25 Mai 2018, 19:00
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Non c'est plutôt,
||2u+3v||=√120 = (2√30)^2
||2u+3v||=√120 = (2√30)^2
- 25 Mai 2018, 17:00
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Donc la réponse à la 2), serait :
||2u+3v||=√120 = (3√30)^2
||2u+3v||=√120 = (3√30)^2
- 25 Mai 2018, 16:53
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Ce nombre vaut (2√30)² car (2√30)²=120 soit √120=(2√30)².
- 25 Mai 2018, 15:04
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
J'ai pas vraiment bien compris comment faire pour en déduire ||2u+3v||.
- 24 Mai 2018, 21:26
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
Re: Exercice, sur les produits scalaires.
Donc pour répondre à la question b)
Faut justifier en disant :
Supposons, w=2u+3v, donc, w.w donc la norme au carré de w, c'est à dire ||w||^2 =120 est alors ||2u+3v||^2
Ainsi le nombre 120, c'est quoi son utilité dans la justification ?
Faut justifier en disant :
Supposons, w=2u+3v, donc, w.w donc la norme au carré de w, c'est à dire ||w||^2 =120 est alors ||2u+3v||^2
Ainsi le nombre 120, c'est quoi son utilité dans la justification ?
- 24 Mai 2018, 21:16
- Forum: ✎✎ Lycée
- Sujet: Exercice, sur les produits scalaires.
- Réponses: 37
- Vues: 5619
- 88 résultats trouvés - Page 4 sur 5 • 1, 2, 3, 4, 5
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
