20 résultats trouvés
Revenir à la recherche avancée
tu peux calculer la densité de Y grâce à l'esperance. tu prends une fonction g continue bornée et on a E[g(Y)] en gros égal en 1er temps (1) \int_{-\infty}^{+\infty}g(x)f_{Y}(x)dx telle que f_{y}(x) est la fonction densité de Y. Et dans un 2eme temps tu as E[g(Y&#...
- 17 Jan 2014, 19:53
- Forum: ✯✎ Supérieur
- Sujet: Aide pour intégrale
- Réponses: 11
- Vues: 794
bonjour je me demandais si ca changeait quelquechose d'inverser l'ordre des vecteurs dans la matrice de passage , par exemple on a deux espaces propres , le 2eme a 2vecteurs propres v2 et v3 , si dans la matrice de passage on met p=(v1 v3 v2) cest la meme chose que p=(v1 v2 v3) ? Merci Logiquement ...
- 11 Déc 2013, 18:31
- Forum: ✯✎ Supérieur
- Sujet: diagonalisation (cas de matrice symetique)
- Réponses: 6
- Vues: 684
Dans le cas d'une diagonalisation. Imagine que \lambda_1 = 1 , \lambda_2 = 2 et \lambda_3 = 3 , ou \lambda_i est la valeur propre associee au vecteur v_i . Si j'appelle p' = (v1 v3 v2), et p = (v1 v2 v3), et D_p la matrice diagonalisee dans la base p, et D_{p'} la matrice diagonalisee dans la b...
- 11 Déc 2013, 18:28
- Forum: ✯✎ Supérieur
- Sujet: diagonalisation (cas de matrice symetique)
- Réponses: 6
- Vues: 684
kmikazi a écrit:Mais M est pas egale à 3, nn?
deplus on en deduit quoi?
c'est un produit matricielle ! matrice 3x3 * matrice 3x1 donne matrice 3x1.
- 09 Déc 2013, 22:11
- Forum: ✯✎ Supérieur
- Sujet: matrice question basique
- Réponses: 8
- Vues: 678
- 09 Déc 2013, 21:25
- Forum: ✯✎ Supérieur
- Sujet: matrice question basique
- Réponses: 8
- Vues: 678
Ben314 a écrit:Comme ça (le plus "naturel" à mon sens) ou comme ça (plus rapide...)
Oui oui c'est bon merci bcp
- 07 Déc 2013, 14:03
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
Ben314 a écrit:Avec la valeur absolue, on trouve +oo.
Donc l'intégrale est "semi convergente" mais n'est pas "absolument convergente" (voir post çi dessus que j'ai ralongé...)
Merci bcp, une dernière question et désolé pour le derangement, c'est que cmt t'as trouvé +oo ?
- 07 Déc 2013, 12:54
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
Ben314 a écrit:Il n'y a pas d'erreur.
Sauf que tu avais dit que "intégrable", pour toi,et que là, tu n'a pas mis la valeur absolue.
Euh oui, t'as raison. Et avec la valeur absolue on trouve quoi ?
- 07 Déc 2013, 12:46
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
OK donc sinx/x n'est pas intégrable sur [1,+infini[ (résultat bien connu) Pour montrer que intégrale(1 à +infini, (|sinx|/x) dx) = +infini tu peux comparer avec la série de terme général Un = intégrale(2npi à 2(n+1)pi, (|sinx|/x)dx ) Montre que Un > K/n où K est une certaine constante Merci, je com...
- 07 Déc 2013, 12:37
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
- 07 Déc 2013, 11:34
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
Bonjour Essaies d'utiliser la règle d'Abel pour les intégrales impropres. Merci de ta réponse rapide, ça parait vraiment logique en utilisant Abel, sachant que 1/x est C^{1} sur [1,+\infty] ainsi qu'elle est décroissante et nulle en +\infty , de plus que \int_{x}^{y}sin(t) dt est bornée pou...
- 07 Déc 2013, 11:33
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
Fonction integrable
Bonjour,
Est ce que/x) est intégrable sur |R.
est intégrable sur |R.
J'ai montré que c'était vrai pour mais il me reste l'intervalle
mais il me reste l'intervalle  que j'ai pas su faire.
que j'ai pas su faire.
Merci
Est ce que
J'ai montré que c'était vrai pour
Merci
- 07 Déc 2013, 10:52
- Forum: ✯✎ Supérieur
- Sujet: Fonction integrable
- Réponses: 14
- Vues: 1094
car j'ai trouvé dans un exo !
je doi 1rement determiner la serie de fourier de exp(x) puis deduire la valeur de$) et
et ^n/(n^2+1)$) enfin deduire
enfin deduire 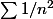
je doi 1rement determiner la serie de fourier de exp(x) puis deduire la valeur de
- 23 Mar 2013, 20:00
- Forum: ✯✎ Supérieur
- Sujet: somme serie 1/n²
- Réponses: 2
- Vues: 773
somme serie 1/n²
bonsoir,
svp comment calculer la serie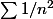 en utilisant la serie
en utilisant la serie $) dont on a la somme.
dont on a la somme.
Merci
svp comment calculer la serie
Merci
- 23 Mar 2013, 19:34
- Forum: ✯✎ Supérieur
- Sujet: somme serie 1/n²
- Réponses: 2
- Vues: 773
Avec les balises TEX. Tu vas dans la partie "Lycée" et il y a un post appelé "Ecrire de belles formules". Sinon tu vas là : http://fr.wikipedia.org/wiki/Aide:Formules_TeX Ensuite quand tu écris avec ces codes là tu sélectionnes tes formules et tu cliques sur le bouton TEX. Merci...
- 24 Déc 2012, 16:43
- Forum: ✯✎ Supérieur
- Sujet: Polynôme scindé
- Réponses: 9
- Vues: 3507
- 24 Déc 2012, 15:30
- Forum: ✯✎ Supérieur
- Sujet: Polynôme scindé
- Réponses: 9
- Vues: 3507
chelsea-asm a écrit:D'accord, je comprends mieux le truc. Mais jusque là je ne trouve pas d'exemple de polynôme non scindé.
X²+1 est non scindé sur R
- 24 Déc 2012, 15:25
- Forum: ✯✎ Supérieur
- Sujet: Polynôme scindé
- Réponses: 9
- Vues: 3507
- 24 Déc 2012, 11:48
- Forum: ✯✎ Supérieur
- Sujet: Exo integrale curviligne complexe
- Réponses: 4
- Vues: 788
Au fait pour la 1re question c'est bon ! j'ai utilisé sin(t)>2*t/pi En ce qui concerne la 2eme question, je ne sais pas où je vais avoir besoin de l'inégalité de la 1re question, car j'ai utilisé la méthode des residus en choisissant le contour de [-R,R] segment + arc pour R>1 pour que le pole i soi...
- 24 Déc 2012, 10:25
- Forum: ✯✎ Supérieur
- Sujet: Exo integrale curviligne complexe
- Réponses: 4
- Vues: 788
Exo integrale curviligne complexe
svp vous pouvez me guider dans cet exo !
Exo
Exo
- 24 Déc 2012, 01:40
- Forum: ✯✎ Supérieur
- Sujet: Exo integrale curviligne complexe
- Réponses: 4
- Vues: 788
- 20 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
