merci à vous pour ces réponses rapides.
Par contre, je trouve que ce n'est pas évident pour tout justifier correctement.
78 résultats trouvés
Revenir à la recherche avancée
- 30 Mar 2010, 10:34
- Forum: ✯✎ Supérieur
- Sujet: oral capes interne
- Réponses: 7
- Vues: 1553
oral capes interne
Bonjour, Je bloque sur ce problème : (d), (d') 2 droites sécantes en dehors de ma feuille. A un point quelconque qui n'est ni sur d ni sur d'. Le professeur Orthocentrus affirme qu'il peut tracer à l'équerre seule la droite passant par le point A et le point d'intersection des droites d et d' sans c...
- 30 Mar 2010, 09:36
- Forum: ✯✎ Supérieur
- Sujet: oral capes interne
- Réponses: 7
- Vues: 1553
merci
si l'on pose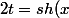) on trouve
on trouve 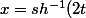) et on trouve les nouvelles bornes en remplaçant t par 1 et -1 sauf que ça ne me paraît pas évident de résoudre
et on trouve les nouvelles bornes en remplaçant t par 1 et -1 sauf que ça ne me paraît pas évident de résoudre =x) ou
ou =x)
si l'on pose
- 13 Déc 2009, 10:26
- Forum: ✯✎ Supérieur
- Sujet: intégrale
- Réponses: 9
- Vues: 366
intégrale
Bonjour,
Comment calculer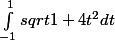 ?
?
Merci
Comment calculer
Merci
- 12 Déc 2009, 17:50
- Forum: ✯✎ Supérieur
- Sujet: intégrale
- Réponses: 9
- Vues: 366
- 02 Jan 2009, 15:08
- Forum: ✯✎ Supérieur
- Sujet: angles orientés
- Réponses: 2
- Vues: 709
angles orientés
Bonjour, Voici mon problème : Dans un plan euclidien P, on considère deux carrés, ABCD et DEFG, de sens direct où E est un point de la droite (CD) autre que C et D. On nomme I l'intersection de (AE) et (BF). Je dois montrer que C,G,I sont alignés. On me propose de montrer que I appartient aux cercle...
- 01 Jan 2009, 18:25
- Forum: ✯✎ Supérieur
- Sujet: angles orientés
- Réponses: 2
- Vues: 709
bonsoir, j'ai besoin d'une indication pour avancer. Je rappelle la situation : Soit un cercle (C) de centre 0 et de rayon R. Soit A un point de P différent de O intérieur à (C). La demi-droite d'origine A passant par O coupe (C) au point B. On prend une equerre dont le sommet est en A. Les côtés de ...
- 16 Déc 2008, 19:28
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
merci Je suis arrivé dans ma preuve en utilisant le fait que (BC) est la bissectrice de l'angle C'CH_1 et en travaillant sur les angles à : (\vec{CC'},\vec{CB})=(\vec{AB},\vec{AH_1}) J'aurais donc dû utiliser à nouveau la bissectrice ici. J'ai bien compris le principe maintenant....
- 14 Déc 2008, 18:42
- Forum: ✯✎ Supérieur
- Sujet: orthocentre
- Réponses: 6
- Vues: 561
bon alors voilà après de multiples tentatives, j'arrive uniquement à montrer que C,A,C',A' sont cocycliques, ce qui ne me convient pas. Si quelqu'un a une idée, merci de me la soumettre...
- 14 Déc 2008, 18:25
- Forum: ✯✎ Supérieur
- Sujet: orthocentre
- Réponses: 6
- Vues: 561
ce ne doit pas être bon tout ça car pour écrire cela, je considère que les 4 points sont déjà cocycliques.
- 14 Déc 2008, 12:39
- Forum: ✯✎ Supérieur
- Sujet: orthocentre
- Réponses: 6
- Vues: 561
ce n'est pas avec l'angle inscrit par hasard. (\vec{BC},\vec{BA})=\frac{1}{2}(\vec{OC},\vec{OA})(\pi) (\vec{H1C},\vec{H1A})=\frac{1}{2}(\vec{OC},\vec{OA})(\pi) d'où (\vec{BC},\vec{BA})=(\vec{H1C},\vec{H1A})(\pi) Les points sont ...
- 14 Déc 2008, 12:34
- Forum: ✯✎ Supérieur
- Sujet: orthocentre
- Réponses: 6
- Vues: 561
orthocentre
Bonjour, Pouvez-vous m'aider à démontrer le théorème suivant : Dans tout triangle non plat, les symétriques de l'orthocentre par rapport aux côtés du triangle se trouvent sur le cercle circonscrit à ce triangle. J'ai appelé H l'orthocentre, H1 H2 et H3 les 3 symétriques par rapport à (AB),(AC) et (B...
- 14 Déc 2008, 11:59
- Forum: ✯✎ Supérieur
- Sujet: orthocentre
- Réponses: 6
- Vues: 561
On me demande maintenant de déterminer le lieu du point H, projeté orthogonal de A sur la droite (PQ).
Faut-il partir comme pour la question précédente en déterminant OH²+AH² ?
Faut-il partir comme pour la question précédente en déterminant OH²+AH² ?
- 13 Déc 2008, 19:09
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
IO²+IA²=R².Soit J le milieu de [OA] \vec{IO}^2+\vec{IA}^2=R^2 (\vec{IJ}+\vec{JO})^2+(\vec{IJ}+\vec{JA})^2=R^2 IJ^2+JO^2+IJ^2+JA^2+2(\vec{IJ}.\vec{JO}+\vec{IJ}. \vec{JA})=R^2 2IJ^2+2JO^2=R^2 d'où IJ=\sqrt{\frac{R^2-2JO^2}{2}} L'ensemble cherché est le cercle de centre J et de ...
- 13 Déc 2008, 18:24
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
- 13 Déc 2008, 17:22
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
- 13 Déc 2008, 16:48
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
Voici la suite du problème : On place une equerre de façon que le sommet de l'angle droit soit en A. Les côtés de l'angle droit coupent le cercle en 2 points P et Q. Déterminer le lieu des points I où I est le milieu de [PQ] lorsque l'équerre tourne autour du point A. On a une indication qui est la ...
- 13 Déc 2008, 16:39
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
- 13 Déc 2008, 16:23
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
géométrie élémentaire (2)
Bonjour, Je suis encore ennuyé par des problèmes avec la géométrie non euclidienne. Voici mon pb : On considère un cercle (C) de centre O et de rayon R. On place un point A strictement intérieur à (C) . La demi-droite d'origine A passant par O coupe le cercle (C) en un point ...
- 13 Déc 2008, 15:52
- Forum: ✯✎ Supérieur
- Sujet: géométrie élémentaire (2)
- Réponses: 9
- Vues: 1017
donc (MG)//(AC) ce qui conclut !
l'ensemble cherché est une droite parallèle à (AC) passant par G
- 12 Déc 2008, 22:05
- Forum: ✯✎ Supérieur
- Sujet: produit vectoriel
- Réponses: 12
- Vues: 1040
- 78 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
