Intégrales et primitives

[Jjl]

Bonjour,j'ai un peu de mal a calculer ces intégrales:
;)x cos(2x) dx ; (3);)x²sin x dx; (1)
;)2*e^(x)(e^(2x) + 1)dx , On posera : t = e^(x)

[deltab]

Bonjour.

Bonjour,j'ai un peu de mal a calculer ces intégrales:
x cos(2x) dx ; (3);)x²sin x dx; (1)
2*e^(x)(e^(2x) + 1)dx , On posera : t = e^(x)

Les 2 premières se calculent très par des IPP.
Je ne sais pas si pour , l'indication "On posera : " fait partie de l'énoncé ou c'est toi qui la suggère comme changement de variables. Il est plus simple de développer l'expression . Que donnera le changement de variable proposé ?

[Jjl]

Bonjour,non je n'ai pas proposer ce changement,c'est dans l'énoncé oups la fonction c'est
;)2*e^(x)/(e^(2x) + 1)dx j'ai fait une erreur désolé et sa primitive c'est Ln(exp(2x)+1)= 2x+1 je crois,mais puisque on a commencé avec la mauvaise fonction on va continué,alors quant on fait un changement de variable on obtient ;)2t(t²+1)dt = ;)2t^(3)+2t= (t^(4))/2 +t². et si c'était l'autre fonction "la vrai" on aurait après le changement de variable: ;)2t/(t²+1) et ça c'est de la forme u'/u donc la primitive c'est Ln(u)=Ln(t²+1). Merci pour ton aide deltab :).

[Ezra]

2*e^(x)(e^(2x) + 1)dx , On posera : t = e^(x)

Quand la fonction à intégrer est où , on a la même forme primitive et à définir...

[Jjl]

Ok mais ce que j'ai écris est faux?

[Jjl]

Ok mais ce que j'ai écris est faux?

[deltab]

Bonjour

Quand la fonction à intégrer est où , on a la même forme primitive et à définir...

On n'a pas la forme , ici n'est pas un polynôme.

Ok mais ce que j'ai écris est faux?

Malheureusement OUI

Le changement de variables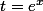 donne et d'où

On aurait eu la forme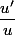 à éventuellement une constante multiplicative près ou .

[Jjl]

Ok merci encore pour ton aide.

[ibtismàth]

quelqu'un pourra m'expliquer ce passage svp :(
\int_{Br(x)}f(y) dy=\int_{0}^{r}\int_{S^{n-1}}f(x+tw)d\sigma (w)t^{n-1}dt.
où Br(x) est la boule ouverte de rayon centré en x et S{n-1} est lasphére unité.