DM pour mardi (équations)

[Evattitude]

J'ai un devoir maison à faire pour mardi, et j'ai du mal pour certaines questions (en gras). Merci !

EXERCICE 2 :
1) Soit f(x)=-6x²+13x-5
a) Vérifier que pour tout réel x on a : f(x)=(2x-1)(5-3x)
b) En déduire les solutions de l'équation f(x)=0
2) g(x)=-12x²+14x+7
a) Vérifier que pour tout réel x on a : f(x)-g(x)=(2x-3)(3x+4)
b) En déduire les solutions de l'équation f(x)=g(x)

EXERCICE 3 :
Factoriser les expressions suivantes (à l'aide des identités remarquables) :
1) A=9x²-12
2) B=(1-3x)(x+1)-(1-3x)²
3) C=(5x+1)(4-3x)+(3x-4)(x-2)
4) D=16(x-2)²-81

[Carpate]

J'ai un devoir maison à faire pour mardi, et j'ai du mal pour certaines questions (en gras). Merci !

EXERCICE 2 :
1) Soit f(x)=-6x²+13x-5
a) Vérifier que pour tout réel x on a : f(x)=(2x-1)(5-3x)
b) En déduire les solutions de l'équation f(x)=0
2) g(x)=-12x²+14x+7
a) Vérifier que pour tout réel x on a : f(x)-g(x)=(2x-3)(3x+4)
b) En déduire les solutions de l'équation f(x)=g(x)

EXERCICE 3 :
Factoriser les expressions suivantes (à l'aide des identités remarquables) :
1) A=9x²-12
2) B=(1-3x)(x+1)-(1-3x)²
3) C=(5x+1)(4-3x)+(3x-4)(x-2)
4) D=16(x-2)²-81

Compare les solutions de et de
1) et 4)
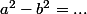
2) et 3) ouvrir l'oeil et répérer les éléments communs

[Evattitude]

Compare les solutions de et de
1) et 4)
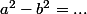
2) et 3) ouvrir l'oeil et répérer les éléments communs

Merci, mais je ne comprends tj pas la 2)b) de l'exo 2..

[Carpate]

Merci, mais je ne comprends tj pas la 2)b) de l'exo 2..

Supposons que est racine de :
ce qui est équivalent à :

donc que est racine de l'équation ... = ...

[Evattitude]

Supposons que est racine de :
ce qui est équivalent à :

donc que est racine de l'équation ... = ...

Je n'ai toujours pas appris le terme "racine".. Je suis en seconde
Désolée :wrong:

[Sourire_banane]

Je n'ai toujours pas appris le terme "racine".. Je suis en seconde
Désolée :wrong:

"Solution" alors, te parlera davantage.

[Evattitude]

"Solution" alors, te parlera davantage.

Oui, mais je ne trouve quand même pas la solution, pouvez me la dire pour que je comprenne ?

[titine]

Tu dois résoudre f(x) = g(x)
C'est à dire f(x) - g(x) = 0
Or au 2a) tu as vu que f(x) - g(x) = (2x-3)(3x+4)
Il faut donc résoudre : (2x-3)(3x+4) = 0
Un produit est égal à 0 si un des facteurs est égal à 0.
Donc (2x-3)(3x+4) = 0 si 2x-3 = 0 ou si 3x+4 = 0
............