TOPOLOGIE définition

[Eya touta]

bsr
O= {Ø};){nZ, n entier } est une topologie sur Z ?

[jlb]

{2Z}U{3Z} est non vide, si c'est une topologie alors tu peux l'écrire comme {kZ} et tu as donc k=1 mais 5=1*5 n'est pas dans {2Z}U{3Z}
Donc, pour moi ce n'est pas une topologie mais bon, c'est à confirmer ( pas vraiment une référence, désolé!!)

[Eya touta]

merci en tout cas

[mrif]

{2Z}U{3Z} est non vide, si c'est une topologie alors tu peux l'écrire comme {kZ} et tu as donc k=1 mais 5=1*5 n'est pas dans {2Z}U{3Z}
Donc, pour moi ce n'est pas une topologie mais bon, c'est à confirmer ( pas vraiment une référence, désolé!!)

Le contre exemple que tu as pris montre bien que l'union des 2 ouverts {2Z} et {3Z} n'appartient pas à O donc n'est pas un ouvert et cela montre bien que O n'est pas une toplologie. Il y a rien à rajouter.

[L.A.]

Bonjour.

Remarque : par contre on peut définir la topologie p-adique (p étant un nombre premier fixé) dont une base d'ouverts sont , et les pour et .

[jlb]

Bonjour.

Remarque : par contre on peut définir la topologie p-adique (p étant un nombre premier fixé) dont les ouverts sont , et les pour .

bonjour et merci pour ces précisions. Par contre, cela est utilisé dans quel but? je suis devenu assez pragmatique et j'aime bien savoir à quoi cela sert. Si jamais tu peux m'éclairer, je t'en remercie.

[L.A.]

correction : en fait c'est une base d'ouverts donnée par , et les pour et 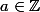. Du coup ma remarque s'éloigne de la question de départ, mais bon c'est une topologie sur Z qu'on utilise en pratique.

D'une part, on peut remarquer que cette topologie est métrisable : on pose



pour x entier (ou rationnel) avec la puissance de p dans la décomposition en facteurs premiers de x, alors la topologie est induite par la distance .

L'utilité réside dans la formule du produit : dans elle s'écrit simplement pour :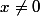



mais elle peut se généraliser à n'importe quel corps de nombres (= extension finie de ). Et on utilise cette relation dans un grand nombre de démonstrations de transcendance (de mémoire, le théorème de Schneider-Lang qui implique le théorème de Lindemann et donc la transcendance de pi).

[Eya touta]

Le contre exemple que tu as pris montre bien que l'union des 2 ouverts {2Z} et {3Z} n'appartient pas à O donc n'est pas un ouvert et cela montre bien que O n'est pas une toplologie. Il y a rien à rajouter.

peux tu svp expliquer le contre exemple ? même s'il parait simple mais j'ai pas compris :triste:

[Sylviel]

Une des pptés d'une topologie c'est que l'union finie d'ouvert doit être un ouvert.

Tes ouverts sont de la forme {n Z}

j'en considère 2 :
{2 Z} et {3 Z}. Est ce que leur union est un ouvert ? Si oui, donne moi le n qui correspond...

[mrif]

peux tu svp expliquer le contre exemple ? même s'il parait simple mais j'ai pas compris :triste:

Regarde la définition d'une topologie sur ce site par exemple:http://fr.wikipedia.org/wiki/Espace_topologique.

Si O était une toplogie, les parties {2Z} et {3Z} seraient des ouverts puisqu'elles appartiennent à la famille définissant la topologie O. Or, dans une topologie, une union quelconque d'ouverts (éléments de O) est un ouvert (c'est à dire appartient à O). Comme il n'existe aucun entier relatif k tel que {2Z} U {3Z} = kZ, l'union {2Z} U {3Z} n'est pas un ouvert et cela constitue un contre exemple puisque si O était une toplogie l'union de 2 ouverts serait un ouvert.

[Eya touta]

ah d'accord , merci à tous

[jlb]

correction : en fait c'est une base d'ouverts donnée par , et les pour et . Du coup ma remarque s'éloigne de la question de départ, mais bon c'est une topologie sur Z qu'on utilise en pratique.

D'une part, on peut remarquer que cette topologie est métrisable : on pose



pour x entier (ou rationnel) avec la puissance de p dans la décomposition en facteurs premiers de x, alors la topologie est induite par la distance .

L'utilité réside dans la formule du produit : dans elle s'écrit simplement pour :



mais elle peut se généraliser à n'importe quel corps de nombres (= extension finie de ). Et on utilise cette relation dans un grand nombre de démonstrations de transcendance (de mémoire, le théorème de Schneider-Lang qui implique le théorème de Lindemann et donc la transcendance de pi).

merci, je vais essayer de comprendre tout cela.