j'ai besoin de votre aide , je bloc sur la deuxième question et du coup je ne peux pas faire les autre .
Une entreprise fabrique des téléviseurs à écran plat . Le cout total de fabrication ( en centime d'euros) de x téléviseurs est : C(x)= 0.02x²+2x+200
PartieA
a) Calculer le cout de fabrication de 50, 100 , et 150 téléviseur .
b)Quel est le montant des charges fixes, c'est-à-dire des charges de l'entreprise même si elle ne produit aucun téléviseur?
c) Calculer le cout moyen ou le cout unitaire U de fabrication de 50 , 100 ,et 150 téléviseurs .
d) Calculer le cout marginal Cm pour 50 téléviseurs produits (c'est-à-dire C(51)-C(50) puis pour 100 téléviseurs et 150 téléviseurs .
C' étant la fonction dérivée de C, calculer C'(50) c'(100) , et c' (150) et comparer Cm et C' dans chaque cas . Que remarquez vous ?
PARTIE B: Etude des fonctions cout marginal et cout moyen
a)En utilisant pour Cm(x) la fonction C'(x) , dresser le tableau de variation de la fonction Cm.
b) Calculer sur l'intervalle (20;500) la dérivée de la fonction cout moyen :
U(x) = (C(x))/x et montrer que : U'(x) = (x²-10000)/50x²
c) Etudier les variations de la fonction cout moyen sur (20;500)
d) Pour quel nombre de téléviseurs, le cout moyen est il minimal ?
e) Tracer les deux fonction U(x) et Cm(x) dans un même repère .
f) Déterminer l'équation de la tangente au point d'abscisse x=50 . La tracer sur le graphique
g) Vérifierque lorsque le cout moyen est minimal alors le cout moyen est égal au cout marginal . Quelle est alors le cout total de la production?
h)De façon général (soit pour toute fonction cout C(x) ) , démontrer , en utilisant l'écriture
U(x)= (C(x))/x , que si U'(x)= 0 alors Cm(x)= U(x)
CE QUE J'AI FAIS
a) C(50)= 0.02*50²+2*50+200
=350
C(100)=0.02*100²+2*100+200
=600
C(150)=0.02*150²+2*150+200
=950
Dérivation
13 messages
- Page 1 sur 1
Oui. En fait, la dérivée d'une fonction de coût est une bonne approximation du coût marginal.
-C(q) \ = \ 0.02(q+1)^2+2(q+1)+200 \ - \ 0.02q^2+2q+200 \ \longleftrightarrow)
+2q+2+200 \ - \ 0.02q^2+2q+200 \ \ \longleftrightarrow)
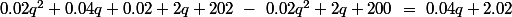
D'où : \ \sim \ C(q+1)-C(q) \ \longleftrightarrow \ 0.04q+2 \ \sim \ 0.04q+2.02)
Tu vois d'où vient la différence (déjà négligeable) de 0.2, maintenant ? en fait, plus la quantité produite sera élevée, plus l'approximation du coût marginal par la dérivée sera bonne.
sera élevée, plus l'approximation du coût marginal par la dérivée sera bonne.
Tu peux faire la suite.
D'où :
Tu vois d'où vient la différence (déjà négligeable) de 0.2, maintenant ? en fait, plus la quantité produite
Tu peux faire la suite.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 203 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
