Vrai-faux

[Curlymela]

Bonjour j'aimerais quelque explications car je ne comprend vraiment pas cette exercice ou du moins je ne vois vraiment pas comment justifier.

Énoncer :
Pour chacune de ces affirmations ci-dessous, préciser si elle est vraie ou fausse. Justifier votre réponse.

1) Si pour tout x > 0 , on a f(x) < ou égale à 2/x alors lim quand x --> + l'infini de f(x) = 0

Voila merci d'avance.

[Kikoo <3 Bieber]

Bonjour j'aimerais quelque explications car je ne comprend vraiment pas cette exercice ou du moins je ne vois vraiment pas comment justifier.

Énoncer :
Pour chacune de ces affirmations ci-dessous, préciser si elle est vraie ou fausse. Justifier votre réponse.

1) Si pour tout x > 0 , on a f(x) + l'infini de f(x) = 0

Voila merci d'avance.

Bonjour,

D'après toi, vrai ou faux ?

[Curlymela]

j'ai pris un exemple vu qu'on sait que x > 0 j'ai pris par exemple x = 2 , je trouve alors f(2) < ou égale a 1 je remarque aussi que plus x est grand plus f(x) se rapproche de 0 donc je pense que la réponse est vraie.

[Kikoo <3 Bieber]

j'ai pris un exemple vu qu'on sait que x > 0 j'ai pris par exemple x = 2 , je trouve alors f(2) < ou égale a 1 je remarque aussi que plus x est grand plus f(x) se rapproche de 0 donc je pense que la réponse est vraie.

Non,

On prend une fonction f qui est plus petite ou égale à 2/x, ça veut dire à ton niveau que sa courbe se trouve toujours en dessous ou est confondue à celle de 2/x. Ce n'est pas rigoureux de dire ceci mais cela te permet de le visualiser.
Une telle fonction tend-elle forcément vers 0 en l'infini ?

[Curlymela]

[quote="Kikoo 0 , la limite de 2/x quand x tend vers + l'infini sera forcément 0 donc si on prend une fonction égale ou plus petite sa limite sera aussi de 0 non ? La chose que je ne comprend pas c'est que la fonction tend vers 0 en l'infini , cela veut-il dire que quand x tend vers l'infini la fonction tend vers 0 ?

[Kikoo <3 Bieber]

Je ne comprend pas ce que tu veux dire si x > 0 , la limite de 2/x quand x tend vers + l'infini sera forcément 0 donc si on prend une fonction égale ou plus petite sa limite sera aussi de 0 non ? La chose que je ne comprend pas c'est que la fonction tend vers 0 en l'infini , cela veut-il dire que quand x tend vers l'infini la fonction tend vers 0 ?

Et si ta fonction est continue sur R+ et qu'elle diverge en l'infini ?

[Curlymela]

Et si ta fonction est continue sur R+ et qu'elle diverge en l'infini ?

je ne comprend pas dsl :help:

[Kikoo <3 Bieber]

Considère la fonction .
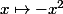
Vois-tu qu'elle est plus petite que la fonction pour tout x de ?
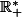
Et pourtant, quel est son comportement en l'infini ?

[Curlymela]

Considère la fonction .
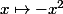
Vois-tu qu'elle est plus petite que la fonction pour tout x de ?
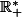
Et pourtant, quel est son comportement en l'infini ?

elle n'a pas de limite

[Kikoo <3 Bieber]

elle n'a pas de limite

Comment ça elle n'a pas de limite ?

[Curlymela]

Comment ça elle n'a pas de limite ?

enfin ca limite serait + l'infini . comment tu répondrais a la question ? j'aurais un exemple pour les autres questions.

[Kikoo <3 Bieber]

enfin ca limite serait + l'infini . comment tu répondrais a la question ? j'aurais un exemple pour les autres questions.

Non non non.
Est-ce que -x² tend vers plus l'infini en l'infini ?

[Curlymela]

Non non non.
Est-ce que -x² tend vers plus l'infini en l'infini ?

Ca veut dire quoi vers plus l'infini en l'infini ?

[Curlymela]

Ca veut dire quoi vers plus l'infini en l'infini ?

-x² tend vers - l'infini en l'infini

[Kikoo <3 Bieber]

-x² tend vers - l'infini en l'infini

Je préfère ça. Donc est-ce que ça tend vers 0 ?

[Curlymela]

Je préfère ça. Donc est-ce que ça tend vers 0 ?

non mais -x² ce n'est pas 2 / x

[Kikoo <3 Bieber]

non mais -x² ce n'est pas 2 / x

Oui ! Mais c'est pas ce qu'on te demande. On te demande si tout fonction inférieure ou égale à 2/x tend vers 0 en l'infini. Tu as ta réponse.

[Curlymela]

Oui ! Mais c'est pas ce qu'on te demande. On te demande si tout fonction inférieure ou égale à 2/x tend vers 0 en l'infini. Tu as ta réponse.

d'accord donc -x² est inférieur a 2/x or -x² tend vers - l'infini en l'infini donc f(x) ne tend pas vers 0 pour la condition f(x) inferieur ou egale a 2/x c'est ca ?

[leon1789]

d'accord donc -x² est inférieur a 2/x or -x² tend vers - l'infini en l'infini donc f(x) ne tend pas forcément vers 0 pour la condition f(x) inferieur ou egale a 2/x c'est ca ?

oui

est-ce que dans ton énoncé, il n'y a pas quelque part écrit que f est une fonction positive ?

[Curlymela]

d'accord donc -x² est inférieur a 2/x or -x² tend vers - l'infini en l'infini donc f(x) ne tend pas vers 0 pour la condition f(x) inferieur ou egale a 2/x c'est ca ?

mais est-ce que si on donne un contre exemple c'est une vraie justification ?