Besoin d'aide pour un vrai/faux (Terminale S)

[Nightmare]

Pour la 3 je suis sceptique, le cours nous dis que si une fonction est continue sur un intervalle alors elle y est dérivable en tout point mais je sens le piège.

Non ! Attention, ton cours ne dit pas ça (ou alors il faut virer ton prof :lol3:). Par contre, il est fort probable qu'il dise le contraire, à savoir qu'une fonction dérivable est continue.

L'inverse est plus que faux. Un contre-exemple simple est la fonction racine carrée, continue en 0 mais pas dérivable en ce point, ou encore la fonction valeur absolue, elle aussi continue en 0 mais pas dérivable. En fait, on a même des fonctions "pathologiques" qui sont continues en tout point et dérivables en aucun (on imagine une courbe en dent-de-scie avec une "pointe" en chaque point).

[Le Twuk]

Non ! Attention, ton cours ne dit pas ça (ou alors il faut virer ton prof :lol3:). Par contre, il est fort probable qu'il dise le contraire, à savoir qu'une fonction dérivable est continue.

L'inverse est plus que faux. Un contre-exemple simple est la fonction racine carrée, continue en 0 mais pas dérivable en ce point, ou encore la fonction valeur absolue, elle aussi continue en 0 mais pas dérivable. En fait, on a même des fonctions "pathologiques" qui sont continues en tout point et dérivables en aucun (on imagine une courbe en dent-de-scie avec une "pointe" en chaque point).

Oui mais la question nous parle du cas ou une fonction est définie sur R. Les contres exemples que vous me donnez sont exacts mais sont ils dérivables sur R ?

Merci

[Nightmare]

Ils ne sont pas dérivables sur R, le but est justement d'exhiber une fonction qui est continue sur R mais n'y est pas dérivable partout. La fonction racine carrée ne convient pas parce que définie seulement sur R+, par contre la valeur absolue convient : Elle est définie et continue sur R mais pas dérivable sur R tout entier (car non dérivable en 0).

Après, comme je te l'ai dit, on peut construire des fonctions continues sur R mais dérivable en aucun point de R mais là ça devient tout de suite d'un autre niveau.

[Le Twuk]

Merci :) Je vais donc dire que a notre niveau nous n'en connaissons pas sur R de non dérivables mais exprimer brièvement que c'est faisable !

Pour la 4 ème j'ai pris la formule du cours, d'après les indications qui m'ont été donné précédemment.

A savoir e(n x a ) = e(a)^n pour tout a réel et n dans Z
Est il alors possible de la transformer en (e^a)^b = e(a^b) pour tout a et b reels

Dans la logique je dirais que oui ...

[Nightmare]

Tu n'as pas besoin de parler de ce contre-exemple pathologique, ça c'était pour ta culture personnelle, tu en fais ce que tu veux :lol3: Tout ce que tu as besoin de dire pour répondre à la question c'est "Faux : Contre-exemple, la fonction valeur absolue est continue sur R mais n'est pas dérivable sur R, car non dérivable en 0". A la limite, ce qui serait éventuellement bon de rajouter, c'est la démonstration que la valeur absolue n'est effectivement pas dérivable en 0. Vois-tu pourquoi?

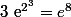
La 4 est clairement fausse. Par exemple avec a=2 et b=3, et ! Et bien entendu,

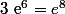
[Le Twuk]

Tu n'as pas besoin de parler de ce contre-exemple pathologique, ça c'était pour ta culture personnelle, tu en fais ce que tu veux :lol3: Tout ce que tu as besoin de dire pour répondre à la question c'est "Faux : Contre-exemple, la fonction valeur absolue est continue sur R mais n'est pas dérivable sur R, car non dérivable en 0". A la limite, ce qui serait éventuellement bon de rajouter, c'est la démonstration que la valeur absolue n'est effectivement pas dérivable en 0. Vois-tu pourquoi?

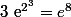
La 4 est clairement fausse. Par exemple avec a=2 et b=3, et ! Et bien entendu,

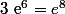
Merci beaucoup C'est vrai que si on prend des chiffres ça devient plus clair !

[Le Twuk]

Pour la 8 je me demande comment on peut bien introduire la fonction inverse pour Un. Est ce qu'il faudrait définir Vn comme 1/Un ? Donc Wn = Vn / Un ?

[Nightmare]

Je ne comprends pas trop ta réflexion sur la question 8.

Encore une fois, on a des contre-exemple simples, par exemple prendre V(n)=1 et U(n)=1/n . Ces deux suites convergent (la première vers 1 et la deuxième vers 0) et pourtant le quotient V(n)/U(n)= 1/(1/n)=n diverge.

[Le Twuk]

Je ne comprends pas trop ta réflexion sur la question 8.

Encore une fois, on a des contre-exemple simples, par exemple prendre V(n)=1 et U(n)=1/n . Ces deux suites convergent (la première vers 1 et la deuxième vers 0) et pourtant le quotient V(n)/U(n)= 1/(1/n)=n diverge.

En effet j'ai bien cherché la complication. Je pensais qu'il fallait trouver une expression de Vn par rapport a Un pour trouver un contre exemple. Mais merci beaucoup

[sad13]

Bonsoir à tous, bien joué "night mare" pr la 1, je sentais le piège mais fallait avoir ce petit contre-exemple classique en tête, ceci dit quand tu dis ""pointe" c'est un point anguleux quoi le sommet de la "dent de scie"

sinon twulk, ceci va te servir si tu le mets ds ta démo
"la démonstration que la valeur absolue n'est effectivement pas dérivable en 0"

et pour la4, le truc c'est qu'il faiut pas la confondre avec la propriété: (exp(a))^b=exp(a*b)

[Le Twuk]

Bonsoir à tous, bien joué "night mare" pr la 1, je sentais le piège mais fallait avoir ce petit contre-exemple classique en tête, ceci dit quand tu dis ""pointe" c'est un point anguleux quoi le sommet de la "dent de scie"

sinon twulk, ceci va te servir si tu le mets ds ta démo
"la démonstration que la valeur absolue n'est effectivement pas dérivable en 0"

et pour la4, le truc c'est qu'il faiut pas la confondre avec la propriété: (exp(a))^b=exp(a*b)

Oui je vais faire attention Merci !

Mais je bloque sur la 10, la dernière rahh !
Je fais des schémas depuis tout a l'heure pour essayer de voir, et surtout que les intégrales, je n'ai pas très bien assimilé encore. En fait dans cette question, ce qui nous est demandé c'est de remarquer qu'il est impossible d'avoir somme de 0 a 1 f(x) dx > somme de 0 a 1 g(x) dx, mais l'aire entre g et f etant toujours plus bas elle sera donc toujours grandement négative, si l'on rapproche les deux courbes elle le sera toujours... Faut il regarder l'aire entre l'axe des abscisses et chacune des courbes ? Ou regarder celle entre les deux courbes. Car dans les deux cas, je ne vois pas comment faire

Merci d'avance.

[Nightmare]

Il faut revenir au cours. Tout ce qu'on a dans celui-ci et qui pourrait nous aider, c'est que si f et g sont positives et telles que alors .

Dans notre problème, f et g sont négatives, mais dans ce cas, -f et -g sont elles positives ! Et en outre, puisque , on a

Alors d'après le cours , puis par linéarité de l'intégrale, on peut sortir les -, donc et donc .

On ne pourra donc jamais avoir l'inégalité inverse !

[Le Twuk]

Il faut revenir au cours. Tout ce qu'on a dans celui-ci et qui pourrait nous aider, c'est que si f et g sont positives et telles que alors .

Dans notre problème, f et g sont négatives, mais dans ce cas, -f et -g sont elles positives ! Et en outre, puisque , on a

Alors d'après le cours , puis par linéarité de l'intégrale, on peut sortir les -, donc et donc .

On ne pourra donc jamais avoir l'inégalité inverse !

C'est bien vu Finallement je me lance toujours dans les mauvaises démonstrations !

Encore merci à vous tous d'avoir porté attention à mon problème et d'avoir usé de votre patience pour m'aider. Je vais travailler tout cela à l'avenir !

[sad13]

Pour la 9, la réciproque est vraie car c'est la positivité de l'intégrale mais ce sens, là, me paraît faux
sans l'ombre d'une doute , il faudrait ,si je me rappelle bien, un point x0 où f(x0)>0 pour que ça soit vrai.

merci

[Nightmare]

Hello,

contre-exemple : sans que x-1/3 ne soit positive sur cet intervalle.

[sad13]

grazie mille, as tu des infos sur le cas où ça marche"il faudrait ,si je me rappelle bien, un point x0 où f(x0)>0 pour que ça soit vrai."

[Nightmare]

Non pas seulement ! L'intégrale d'une fonction continue, c'est l'aire située entre la courbe est l'axe des abscisses, positive si la courbe est au dessus de l'axe, négative si la courbe est en dessous.

Pour construire un contre-exemple, il suffit de trouver une fonction dont l'aire située au dessus de sa partie négative est inférieure à l'aire située en dessous de sa partie positive, la somme des deux sera alors positive. C'est ce que j'ai fait avec x-1/3.

[sad13]

Ok merci

"la somme des deux sera alors positive." en gros une fonction non positive partout mais dont l'aire est positive et l'aire de sa partie négative étant négative, il faut qu'elle soit < à celle de sa partie positive car l'aire des deux c'est la somme des aires.

je crois que je confonds avce un autre théorème que j'avais vu dans Monier, àça doit être du style si l'intégrale de f est >=0, f continue, positive et il existe un point où f est strictement positive alors l'intégrale de f est >0.

merci