Calcul integral
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 08:56
par Inogood » 14 Avr 2012, 08:56
Bonjour Forum,
Je me retrouve bloque très rapidement dans cet exo :
On a, pour tout entier naturel n

1,
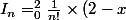^n \times e^x dx)
A/ Calculer
B/ Établir que pour tout entier naturel n

1, on a 0

)
C/ A l'aide d'une integration par parties, montrer que tout pour tout entier naturel n

1 on a :
!})
=========
Pour la A, je trouve :
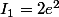
est-ce juste ?
Pour la B, je calcules

et
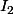
? Je ne sais comment faire...
Pour la C, j'aurai besoin dêtre éclairci...
Merci d'avance !
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 14 Avr 2012, 10:09
par Manny06 » 14 Avr 2012, 10:09
Inogood a écrit:Bonjour Forum,
Je me retrouve bloque très rapidement dans cet exo :
On a, pour tout entier naturel n

1,
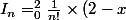^n \times e^x dx)
A/ Calculer
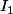
B/ Établir que pour tout entier naturel n

1, on a 0

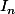
)
C/ A l'aide d'une integration par parties, montrer que tout pour tout entier naturel n

1 on a :
!})
=========
Pour la A, je trouve :
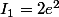
est-ce juste ?
Pour la B, je calcules

et
? Je ne sais comment faire...
Pour la C, j'aurai besoin dêtre éclairci...
Merci d'avance !
pour I1 je trouve e²-3
pour la 2) encadre (2-x)^n sur l'intervalle [0;2]
on verra le reste après
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 14 Avr 2012, 10:41
par geegee » 14 Avr 2012, 10:41
Inogood a écrit:Bonjour Forum,
Je me retrouve bloque très rapidement dans cet exo :
On a, pour tout entier naturel n

1,
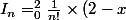^n \times e^x dx)
A/ Calculer
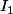
B/ Établir que pour tout entier naturel n

1, on a 0

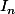
)
C/ A l'aide d'une integration par parties, montrer que tout pour tout entier naturel n

1 on a :
!})
=========
Pour la A, je trouve :
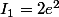
est-ce juste ?
Pour la B, je calcules

et
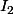
? Je ne sais comment faire...
Pour la C, j'aurai besoin dêtre éclairci...
Merci d'avance !
Bonjour,
I1 = integrale(de 0 à 2) (1/1)*(2-x)^1 * e^x dx
I1=[(2-x)*e^x]0,2 - [(-1)*e^x]0,2 =e^2-1-3=....

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Avr 2012, 11:17
par chan79 » 14 Avr 2012, 11:17
Manny06 a écrit:pour I1 je trouve e²-3
pour la 2) encadre (2-x)^n sur l'intervalle [0;2]
on verra le reste après
Salut
Je confirme e²-3 pour I1
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 11:23
par Inogood » 14 Avr 2012, 11:23
Pouvez vous detaillez la primite de l'integrale dans la A, car en appliquant ce que je sais, je ne trouve pas ce que vous trouvez :/
Pour la B je tombe sur :
0 ;) 1/n!*(2-x)^n ;) 2^n/n!
0 ;) 1/n!*(2-x)^n * e^x ;) 2^n/n! * e^x
Et je ne trouve pas ce que je cherche...
Pour la C :
u(x)=(2-x)^n donc u'(x)=(-1)^n
v'(x)=e^x donc v(x)= e^x
[uv]0;2 - I(0;2)u'v
[(2-2)^n - (2-0)^n] - I(0;2) (-1)^n*e^x
[0^n - 2^n] - I(0;2) (-1)^n*e^x
-2^n - I(0;2) (-1)^n*e^x
Et je crois que je me suis trompée...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Avr 2012, 12:31
par chan79 » 14 Avr 2012, 12:31
Inogood a écrit:Pouvez vous detaillez la primite de l'integrale dans la A, car en appliquant ce que je sais, je ne trouve pas ce que vous trouvez :/
Pour la B je tombe sur :
0

1/n!*(2-x)^n

2^n/n!
0

1/n!*(2-x)^n * e^x

2^n/n! * e^x
Et je ne trouve pas ce que je cherche...
Pour la C :
u(x)=(2-x)^n donc u'(x)=(-1)^n
v'(x)=e^x donc v(x)= e^x
[uv]0;2 - I(0;2)u'v
[(2-2)^n - (2-0)^n] - I(0;2) (-1)^n*e^x
[0^n - 2^n] - I(0;2) (-1)^n*e^x
-2^n - I(0;2) (-1)^n*e^x
Et je crois que je me suis trompée...
pour le A
e^x est une primitive de e^x
xe^x - e^x est une primitive de x e^x
Ca devrait t'aider
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 12:33
par Inogood » 14 Avr 2012, 12:33
chan79 a écrit:pour le A
e^x] est une primitive de e^x
xe^x - e^x est une primitive de x e^x
Ca devrait t'aider
Oui merci c'est bon ! J'ai trouve. Peux tu m'aider pour la B et C ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 14 Avr 2012, 12:35
par Manny06 » 14 Avr 2012, 12:35
Inogood a écrit:Oui merci c'est bon ! J'ai trouve. Peux tu m'aider pour la B et C ?
pour la B) intègre ta double inégalité
pour la C) la derivée de u est fausse
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 12:41
par Inogood » 14 Avr 2012, 12:41
Manny06 a écrit:pour la B) intègre ta double inégalité
pour la C) la derivée de u est fausse
Merci. En fait pour la A, j'ai encore faux...
Pour I1 vers la fin je tombe sur :


)


Ou me suis-je trompé ?
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 12:42
par Inogood » 14 Avr 2012, 12:42
Et la dérivée de u c'est (n(-(x-2))^n)/(x-2) ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Avr 2012, 12:56
par chan79 » 14 Avr 2012, 12:56
Inogood a écrit:Et la dérivée de u c'est (n(-(x-2))^n)/(x-2) ?
pour la A
une primitive est
g(x)=2e^x-(xe^x-e^x)
g(2)=2e²-2e²+e²=e²
g(0)=2+1=3
le résultat du A est e²-3
pour le B
quand x est compris entre 0 à 2 , (2-x) est lui aussi compris entre 0 et 2
(2-x)^n est inférieur ou égal à 2^n
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 14 Avr 2012, 17:33
par Manny06 » 14 Avr 2012, 17:33
pour I1
(2-x)=u -1=u'
e^x=v' e^x=v
I=[(2-x)e^x]entre 0 et2 +integrale de 0 à2 de e^x dx =-2 +e²-1
il y a une erreur de signe devant ta dernière intégrale
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 17:41
par Inogood » 14 Avr 2012, 17:41
C'est bon j'ai réussi merci. Pour la C, j'ai du mal par contre...
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 18:35
par Inogood » 14 Avr 2012, 18:35
Je prends In, je pose u(x)= (2-x)^n et v'(x)= e^x donc u'(x) = n(2-x)^(n-1) et v(x)= e^x ???
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 14 Avr 2012, 21:41
par Manny06 » 14 Avr 2012, 21:41
Inogood a écrit:Je prends In, je pose u(x)= (2-x)^n et v'(x)= e^x donc u'(x) = n(2-x)^(n-1) et v(x)= e^x ???
il manque encore un signe -
la derivée de (2-x)^n est -n(2-x)^(n-1) (car la derivée de 2-x est -1)
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 21:47
par Inogood » 14 Avr 2012, 21:47
Manny06 a écrit:il manque encore un signe -
la derivée de (2-x)^n est -n(2-x)^(n-1) (car la derivée de 2-x est -1)
Meme en changeant je ne trouve pas ce que je suis suppose trouver... pourriez vous m'aidez ?
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 14 Avr 2012, 22:13
par Inogood » 14 Avr 2012, 22:13
Manny06 a écrit:il manque encore un signe -
la derivée de (2-x)^n est -n(2-x)^(n-1) (car la derivée de 2-x est -1)
Meme en changeant je ne trouve pas ce que je suis suppose trouver... pourriez vous m'aidez ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 15 Avr 2012, 09:14
par Manny06 » 15 Avr 2012, 09:14
[quote="Inogood"]Meme en changeant je ne trouve pas ce que je suis suppose trouver... pourriez vous m'aidez ?[/Q
(1/n!)(2-x)^n=u e^x=v'
-(1/(n-1)!)(2-x)^(n-1)=u' e^x=v
In=[(1/n!)(2-x)^ne^x]entre 0 et 2 +integrale de 0 à 2 de(1/(n-1)!)(2-x)^(n-1)e^x
soit
In=-2/n!+In-1

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Avr 2012, 09:46
par chan79 » 15 Avr 2012, 09:46
Manny06 a écrit: Inogood a écrit:Meme en changeant je ne trouve pas ce que je suis suppose trouver... pourriez vous m'aidez ?[/Q
(1/n!)(2-x)^n=u e^x=v'
-(1/(n-1)!)(2-x)^(n-1)=u' e^x=v
In=[(1/n!)(2-x)^ne^x]entre 0 et 2 +integrale de 0 à 2 de(1/(n-1)!)(2-x)^(n-1)e^x
soit
In=-2/n!+In-1
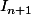
=
!}(2-x)^{n+1}.e^{x}dx)
=
!}\bigint_{0}^{2}(2-x)^{n+1}.e^{x}dx)
=
u=
^{n+1})
donc u'=-
.(2-x)^n)
v'=

donc v=

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
