thiben63 a écrit:Alors j'ai essayer de me guider via un exemple du profs, je m'excuse mais j'ai vraiment du mal a comprendre avec des cours, je comprend plus facilement avec des exercices fait ou je peux voir les procédures ect
Salut !
1) Tes valeurs pour
et
ne sont pas correctes.
En effet, d'après la question, on va calculer une intégrale et en donner le sens géométrique d'après ce qu'on veut faire d'après l'énoncé. Donc en fait, ta parabole aura pour équation,
(c'est la fonction qui est dans l'intégrale).
Pour le prouver, il te suffit simplement de prendre deux points :
Le point
)
appartient à la parabole, donc tu peux trouver
;
Le point
)
appartient à la parabole, donc tu en déduis
:+++:
(L'avantage avec les points dont une des deux coordonnées est nulle est de simplifier grandement les calculs).
2) Ce qu'il ne faut pas perdre à l'esprit, c'est que "primitiver" une fonction consiste à effectuer le "processus" inverse de celui de la dérivation. En effet, si
la dérivée de
est
, alors
une primitive de
est
(la dérivée d'une fonction est unique, mais sa primitive non car elle fait resortir une constante).
Par exemple, la dérivée de
est
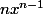
et une primitive de
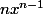
est
.
Je te rappelle qui si l'on a une primitive
d'une fonction
, alors on a :
[CENTER]
\ {\rm d}x= [F(x)]_a^b)
[/CENTER]
Dérivées et primitives ont donc la même propriété de linéarité :
- la dérivée d'une somme de fonctions, c'est la somme des dérivées de ces fonctions, donc une primitive d'une somme de fonctions est la somme des primitives de ces fonctions :
[CENTER]
+g(x))\ {\rm d}x= \int_a^b f(x)\ {\rm d}x + \int_a^b g(x)\ {\rm d}x)
[/CENTER]
- la dérivée du produit d'une fonction par une constante est le produit de cette même constante par la dérivée de la fonction, donc la primitive du produit d'une fonction par une constante est le produit de cette même constante par la primitive de la fonction
[CENTER]
)\ {\rm d}x= \lambda \times \int_a^b f(x)\ {\rm d}x)
[/CENTER]
Donc ici tu as :
[CENTER]
\ {\rm d}x= - \frac 4 9 \int_0^3 x^2\ {\rm d}x + 4 \int_0^3 1\ {\rm d}x)
[/CENTER]
Pour trouver une primitive de
avec
un entier quelconque, il suffit de regarder ce qui se passe lorsqu'on dérive
:
La dérivée de
est
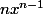
donc une primitive de
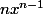
est
, et par conséquent, une primitive de
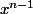
est
.
En remplaçant
par
, on en déduit qu'une primitive de
est
.
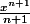
Ainsi, une primitive de
est
(on peut le vérifier en dérivant
).
Je te laisse poursuivre tes calculs :+++:
voila ce que j'ai réussir a faire je pense que le 2) est faux ?
