Dérivée d'une fonction.

[rayane2]

Bonjour.
en ce moment on etudie la derivation et on a vu presque toutes les derivées des fonctions usuelles ainsi que celles des operations (multiplication, addition ...).
j' ai un exercice à faire dont le but est de trouver la dérivée de la fonction suivante:
h(x)= x^5/5 - x^4/4 - 5x^2 /4.
je connais la dérivée de x^5 et celle de 5 ou encore celle de 5x^2 et 1/x^n mais a ce type de fonction je bloque un peu :doh: . :help:
Merci pour vos réponses :id:
Et j'ai une deuxieme dérivée à trouver : celle de (2x+3)/(x+4) => je l'ai trouvée = 11/(x^2+8x+16) mais lorsque on me demande de préciser un intervalle sur lequel elle est dérivable moi je dirais qu'elle est dérivable sur R sauf que je n 'en suis pas sur.
merci.

[manoa]

Salut ^^

quelle est la dérivée de ? (avec a constante et n de N*)

[rayane2]

la dérivée de ax^n = a*nx^n-1
exemple: f(x)= 2x^3 f ' (x) =2*3x^2 soit 6x^2.

[manoa]

la dérivée de ax^n = a*nx^n-1
exemple: f(x)= 2x^3 f ' (x) =2*3x^2 soit 6x^2.

Bien, je ne vois donc pas pourquoi ce type de fonctions te crée problème,ce sont de gentils polynômes ^^


qu'est ce que ça donne en utilisant la dérivée de ax^n ?

Pour la seconde fonction moi je trouve 5/(machin),je pense que tu as loupé un signe moins au numérateur.

Pour le Df il faut éliminer les valeurs interdites.

[rayane2]

Bien, je ne vois donc pas pourquoi ce type de fonctions te crée problème,ce sont de gentils polynômes ^^


qu'est ce que ça donne en utilisant la dérivée de ax^n ?

Pour la seconde fonction moi je trouve 5/(machin),je pense que tu as loupé un signe moins au numérateur.

Pour le Df il faut éliminer les valeurs interdites.

pour la 1ere la dérivée de 1/5 =0 donc au final on trouve = 0 ??

[manoa]

pour la 1ere la dérivée de 1/5 =0 donc au final on trouve = 0 ??

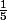
nop, est de forme ax^n (si on prend a= et n=5) ..

[rayane2]

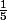
nop, est de forme ax^n (si on prend a= et n=5) ..

Ah oui .. donc au final ca nous donne 5x^4 /5 - 4x^3 /4 -10x/4.

[rayane2]

pour la 2eme vous etes sur que c'est 5/... ? car moi j'ai verifié au moins 3 fois mon developpement et je ne trouve aucune anomalie o.O.

[manoa]

pour la 2eme vous etes sur que c'est 5/... ? car moi j'ai verifié au moins 3 fois mon developpement et je ne trouve aucune anomalie o.O.

Tu me rappelle (u/v)' .

[rayane2]

Tu me rappelle (u/v)' .

(u/v)' = u'v-uv' / v^2

[manoa]

(u/v)' = u'v-uv' / v^2

OK, et que donne (2x+3)'(x+4)-(2x+3)(x+4)' ?

[rayane2]

OK, et que donne (2x+3)'(x+4)-(2x+3)(x+4)' ?

ca nous donne 2(x+4)-(2x+3)*1 => 2x+8-2x+3 =>8+3 = 11

[manoa]

ca nous donne 2(x+4)-(2x+3)*1 => 2x+8-2x+3 =>8+3 = 11

Attention au développement de -(2x+3) !

[rayane2]

Attention au développement de -(2x+3) !

C'est vrai je me suis trompé betement! ...

[rayane2]

pour la premiere j'ai trouvé la dérivée = 5x^4 /5 - 4x^3 /4 - 10x /4
ca reste comme ca ??

[manoa]

Tu peux simplifier ..

Que trouves-tu pour l'intervalle ? ^^

[rayane2]

Tu peux simplifier ..

Que trouves-tu pour l'intervalle ? ^^

je n'arrive pas a trouver le df :mur:

[rayane2]

Pour la simplification j'ai eu : x^4 - x^3 - 5x/2

[manoa]

Pour la simplification j'ai eu : x^4 - x^3 - 5x/2

OK

Pour le domaine, tu dois avoir que toute fonction rationnelle est dérivable sur son domaine de définition, quelle est la valeur interdite pour laquelle n'est pas définie ?

[rayane2]

Ah c'est bon je sais : le df : R- (-4)