Intégration

par **sarah_adams** » 21 Déc 2011, 22:17

Bonjour,
Ma question est la suivante:
je dois montrer que

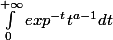
est finie, pour a>0.
je ne sais pas si ma méthode est correcte. Pourriez-vous réctifier s'il vous plait.

Il y a 2 points incertains:

et

Il faut montrer que

existe au voisinage de chaque point incertain.

Au voisinage de 0,

converge ssi a>0 (Riemann). donc intégrale existe.
Au voisinage de l'infinie, j'ai fait une majoration et elle diverge si a>0 (toujours Riemann). donc l'intégrale n'existe pas?

donc j'arrive pas montrer ce qu'on demande..
merci de votre réponse.

par **Monsieur23** » 21 Déc 2011, 22:20

Aloha,

Riemann, c'est bien pour le t^(a-1), mais n'oublie pas l'exponentielle!

par **sarah_adams** » 21 Déc 2011, 22:27

bonjour,
mais je ne vois pas où exactement j'ai fait l'erreur.
Au voisinage de 0, on peut oublier l'exponentielle.
Au voisinage de l'infinie je majore l'exponentielle par 1

maerci de me répondre.

par **Monsieur23** » 21 Déc 2011, 23:14

Si l'exp est là, il faut s'en servir.

Que penses-tu de montrer que ta fonction est un petit o de 1/t^2 en l'infini ?

Intégration

intégration

Qui est en ligne